题目内容
6.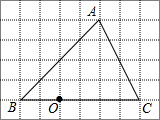 如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是$\sqrt{5}$.
分析 (1)利用OA,利用网格特点,分别画出OA、OB、OC的中点A′、B′、C′,则△A′B′C′满足条件;
(2)利用勾股定理计算出OA的长,然后利用点A′为OA的中点可得到线段AA′的长度.
解答 解:(1)如图,△A′B′C′为所作;
(2)OA=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵OA′:OA=1:2,
∴点A′为OA的中点,
∴AA′=$\sqrt{5}$.
故答案为$\sqrt{5}$.
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
相关题目
1.下列命题中正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 菱形的周长等于两条对角线长之和的两倍 | |
| C. | 对角线相等的平行四边形是菱形 | |
| D. | 菱形的面积等于两条对角线长之积的一半 |
18.若$\sqrt{x-1}+\sqrt{x+y}=0$,则x2015+y2016的值( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
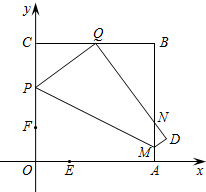 如图,四边形OABC为正方形,点A在x轴上,点C在y轴上,点B(8,8),点P在边OC上,点M在边AB上.把四边形OAMP沿PM对折,PM为折痕,使点O落在BC边上的点Q处.动点E从点O出发,沿OA边以每秒1个单位长度的速度向终点A运动,运动时间为t,同时动点F从点O出发,沿OC边以相同的速度向终点C运动,当点E到达点A时,E、F同时停止运动.
如图,四边形OABC为正方形,点A在x轴上,点C在y轴上,点B(8,8),点P在边OC上,点M在边AB上.把四边形OAMP沿PM对折,PM为折痕,使点O落在BC边上的点Q处.动点E从点O出发,沿OA边以每秒1个单位长度的速度向终点A运动,运动时间为t,同时动点F从点O出发,沿OC边以相同的速度向终点C运动,当点E到达点A时,E、F同时停止运动.