题目内容
3. 如图,AD是等边三角形BC边上的高,以AD为边作等边三角形△ADE,连结BE.
如图,AD是等边三角形BC边上的高,以AD为边作等边三角形△ADE,连结BE.求证:BE⊥AE.
分析 根据等边三角形的性质得到AE=AD,AB=AC,∠BAC=∠DAE=60°,于是得到∠EAB=∠DAC,推出△AEB≌△ADC,得到∠AEB=∠ADC=90°,即可得到结论.
解答 解:∵△ABC与△ADE是等边三角形,
∴AE=AD,AB=AC,∠BAC=∠DAE=60°,
∴∠EAB=∠DAC,
在△AEB与△ADC中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAB=∠DAC}\\{AB=AC}\end{array}\right.$,
∴△AEB≌△ADC,
∴∠AEB=∠ADC,
∵AD是等边三角形BC边上的高,
∴∠ADC=90°,
∴∠AEB=90°,
∴BE⊥AE.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.若a<1,则化简1-a+|a-1|等于( )
| A. | 2-2a | B. | 2a | C. | 2 | D. | 0 |
 已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.
已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.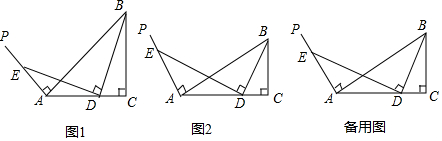
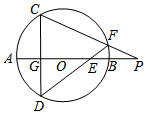 (如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.
(如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2. 小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.
小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.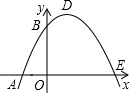 如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)