题目内容
8.解三元一次方程组:$\left\{\begin{array}{l}{x+y+z=2}\\{x-2y+z=-1}\\{x+2y+3z=-1}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x+y+z=2①}\\{x-2y+z=-1②}\\{x+2y+3z=-1③}\end{array}\right.$,
①×2+②得:x+z=1④,
②+③得:x+2z=-1⑤,
⑤-④得:z=-2,
把z=-2代入④得:x=3,
把x=3,z=-2代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=1}\\{z=-2}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
13. 如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )
如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )
 如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )
如图,AB是⊙O的直径,A,C,D在圆上,∠D=65°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
20.若xmyn÷x3y=x2y,则m、n的值为( )
| A. | m=5,n=0 | B. | m=6,n=0 | C. | m=5,n=2 | D. | m=6,n=2 |

 如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO:BO=3,则反比例函数的解析式为y=-$\frac{4}{x}$.
如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO:BO=3,则反比例函数的解析式为y=-$\frac{4}{x}$.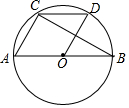 如图,AB为⊙O的直径,菱形AODC的顶点A,C,D在⊙O上,连接BC,则∠ABC的度数为30°.
如图,AB为⊙O的直径,菱形AODC的顶点A,C,D在⊙O上,连接BC,则∠ABC的度数为30°.