题目内容
16. 如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO:BO=3,则反比例函数的解析式为y=-$\frac{4}{x}$.
如图,直线y=-x+3与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO:BO=3,则反比例函数的解析式为y=-$\frac{4}{x}$.
分析 根据一次函数图象上点的坐标特征可求出点A的坐标,结合AO:BO=3可得出BO的长度,进而可得出点C的坐标,再利用反比例函数图象上点的坐标特征即可求出反比例函数的解析式,此题得解.
解答 解:当x=0时,y=3,
∴点A的坐标为(0,3),
∴OA=3.
∵AO:BO=3,
∴BO=1.
当x=-1时,y=-(-1)+3=4,
∴点C的坐标为(-1,4).
∵点C在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=-1×4=-4,
∴反比例函数的解析式为y=-$\frac{4}{x}$.
故答案为:y=-$\frac{4}{x}$.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征以及反比例函数图象上点的坐标特征,根据点C的坐标利用反比例函数图象上点的坐标特征求出反比例函数解析式是解题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
7.下列各组单项式中,不是同类项的是( )
| A. | 1与-6 | B. | $\frac{1}{2}$a3b与2ba3 | C. | -2x2y3与y3x2 | D. | 2xy2与x2y |
11.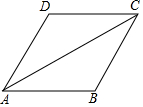 如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )
如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )
 如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )
如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )| A. | 3 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
1. 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
5.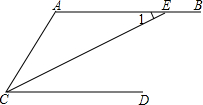 已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )
已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )
 已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )
已知AB∥CD,CE平分∠ACD,交AB于点E,∠1=28°,则∠A的度数为( )| A. | 56° | B. | 62° | C. | 118° | D. | 124° |
8.以下代数式书写规范的是( )
| A. | (x+y)÷2 | B. | 1$\frac{1}{3}$x | C. | $\frac{6}{5}$y | D. | m+n厘米 |
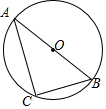 如图,AB是⊙O的直径,点C在圆上,且∠ABC=50°,则∠BAC=40°.
如图,AB是⊙O的直径,点C在圆上,且∠ABC=50°,则∠BAC=40°.