题目内容
20．抛物线y=-x2+bx+c经过点A（-1，0），B（3，0），C（0，m），D（4，n），则m，n的大小关系为m＞n（填“＞”“=”或“＜”）分析 由于A（-1，0）、B（-3，0）为抛物线上的两对称点，则可得到抛物线的对称轴为直线x=1，根据当抛物线开口向下时，抛物线上的点离对称轴越远，对应的函数值越小，得到m＞n．
解答 解：∵y=-x2+bx+c经过点A（-1，0）、B（3，0），
∴抛物线的对称轴为直线x=1，
∵抛物线开口向下，C点（0，m）到直线x=1的距离为1，D点（4，n）到直线x=1的距离为3，
∴m＞n．
故答案为＞．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示的几何体是由五个完全相同的正方体组成的，与这个几何体的主视图不相同的是（ ）
11．
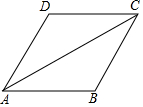如图，菱形ABCD的周长是24，∠BAD=60°，则对角线AC的长等于（ ）
如图，菱形ABCD的周长是24，∠BAD=60°，则对角线AC的长等于（ ）| A． | 3 | B． | 6 | C． | 3$\sqrt{3}$ | D． | 6$\sqrt{3}$ |
15．一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开图的扇形的圆心角是（ ）
| A． | 120° | B． | 180° | C． | 240° | D． | 300° |
5．
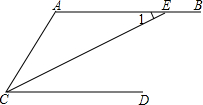已知AB∥CD，CE平分∠ACD，交AB于点E，∠1=28°，则∠A的度数为（ ）
已知AB∥CD，CE平分∠ACD，交AB于点E，∠1=28°，则∠A的度数为（ ）| A． | 56° | B． | 62° | C． | 118° | D． | 124° |
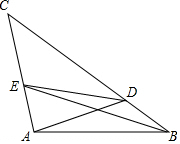△ABC中，D在BC上，E在AC上，∠BAC=100°，∠ABC=40°，∠BAC=20°，∠ABE=20°，则∠ADE=30°．