题目内容
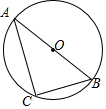
13．
如图，AB是⊙O的直径，A，C，D在圆上，∠D=65°，则∠ABC的度数为（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 35° |
分析 由于AB是⊙O的直径，由圆周角定理可知∠ACB=90°，则∠A和∠ABC互余，欲求∠ABC需先求出∠A的度数，已知了同弧所对的圆周角∠CDB的度数，则∠A=∠CDB，由此得解．
解答 解：∵AB是⊙O的直径，
∴∠ACB=90°，即∠A+∠ABC=90°；
又∵∠A=∠CDB=65°，
∴∠ABC=90°-∠A=25°．
故选B．
点评 此题主要考查的是圆周角定理及其推论；半圆（弧）和直径所对的圆周角是直角；同弧所对的圆周角相等．
练习册系列答案
阅读快车系列答案
相关题目
如图，AB是⊙O的直径，点C在圆上，且∠ABC=50°，则∠BAC=40°．
1．
如图，在平面直角坐标系xOy中，已知点A（2，1）和点B（3，0），则sin∠AOB的值等于（ ）
如图，在平面直角坐标系xOy中，已知点A（2，1）和点B（3，0），则sin∠AOB的值等于（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{2}$ |
5．
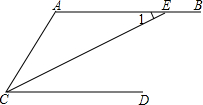已知AB∥CD，CE平分∠ACD，交AB于点E，∠1=28°，则∠A的度数为（ ）
已知AB∥CD，CE平分∠ACD，交AB于点E，∠1=28°，则∠A的度数为（ ）| A． | 56° | B． | 62° | C． | 118° | D． | 124° |
4．下列说法正确的有（ ）
| A． | a一定是正数 | B． | $\frac{7}{3}$是有理数 | ||
| C． | 0.5不是有理数 | D． | 平方等于自身的数只有1个 |
如图，△ABC与△ADE关于直线MN对称，BC与DE的交点F在直线MN上．