题目内容
3．
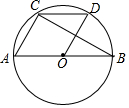如图，AB为⊙O的直径，菱形AODC的顶点A，C，D在⊙O上，连接BC，则∠ABC的度数为30°．
分析 连接OC，根据菱形的性质求出AC=AO，求出△AOC是等边三角形，求出∠A=60°，根据圆周角定理求出∠ACB，即可求出答案．
解答 解：
连接OC，
∵四边形AODC是菱形，
∴AC=AO，
∵OA=OC，
∴AC=AO=OC，
∴△AOC是等边三角形，
∴∠A=60°，
∵AB为直径，
∴∠ACB=90°，
∴∠ABC=90°-60°=30°，
故答案为：30°．
点评 本题考查了菱形的性质，等边三角形的性质和判定，圆周角定理的应用，能熟练地运用定理进行推理是解此题的关键，注意：菱形的四条边都相等．
练习册系列答案
春雨教育同步作文系列答案
相关题目
如图，在△ABC中，∠ACB=90°，AB=5，tanA=$\frac{1}{2}$，将△ABC沿直线l翻折，恰好使点A与点B重合，直线l分别交边AB、AC于点D、E；
如图，点C坐标为（2，0），∠ACO=90°，∠AOC=60°，双曲线y=$\frac{k}{x}$在第一象限内的图象经过OA边的中点B，则k=$\sqrt{3}$．
11．
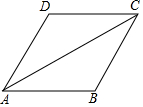如图，菱形ABCD的周长是24，∠BAD=60°，则对角线AC的长等于（ ）
如图，菱形ABCD的周长是24，∠BAD=60°，则对角线AC的长等于（ ）| A． | 3 | B． | 6 | C． | 3$\sqrt{3}$ | D． | 6$\sqrt{3}$ |
如图，在?ABCD中，点E、F在AC上，且AE=CF．求证：四边形BEDF是平行四边形．
15．一个圆锥的侧面积是底面积的3倍，则圆锥侧面展开图的扇形的圆心角是（ ）
| A． | 120° | B． | 180° | C． | 240° | D． | 300° |