题目内容
14. 一次函数y1=3x+4和函数y2=2x+1的图象如图所示,解答下列问题:
一次函数y1=3x+4和函数y2=2x+1的图象如图所示,解答下列问题:(1)求函数y=3x+4和函数y=2x+1的交点坐标;
(2)根据图象回答:
①x取何值时,y1=y2?
②x取何值时,y1>y2?
③x取何值时,y1<y2?
分析 (1)联立得到方程组$\left\{\begin{array}{l}{y=3x+4}\\{y=2x+1}\end{array}\right.$,求出方程组的解,即为交点坐标;
(2)①x=-3,y1=y2;
②x>-3,y1>y2;
③x<-3,y1<y2.
解答 解:(1)联立得到方程组$\left\{\begin{array}{l}{y=3x+4}\\{y=2x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-3}\\{y=-5}\end{array}\right.$
∴函数y=3x+4和函数y=2x+1的交点坐标为(-3,-5);
(2)①x=-3,y1=y2;
②x>-3,y1>y2;
③x<-3,y1<y2.
点评 本题考查了一次函数与一元一次不等式,解决本题的关键是求出交点坐标.

练习册系列答案
相关题目
4. 右边几何体的俯视图是( )
右边几何体的俯视图是( )
 右边几何体的俯视图是( )
右边几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ |
19.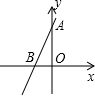 如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
 如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )| A. | x<-2 | B. | -2<x<-1 | C. | -2<x<0 | D. | -1<x<0 |
6.2015年髙考已经结束,南平市教研室从各校随机抽取1000名考生的数学试卷进行调査分析,这个问题的样本容量是( )
| A. | 1000 | B. | 1000名 | ||
| C. | 1000名学生 | D. | 1000名考生的数学试卷 |
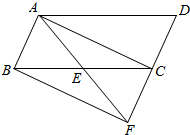 如图,在?ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.
如图,在?ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F. 一张长对边平行的纸条按如图所示方法折叠,则∠1=65°.
一张长对边平行的纸条按如图所示方法折叠,则∠1=65°.