题目内容
2.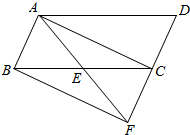 如图,在?ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.
如图,在?ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.(1)求证:CF=CD;
(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
分析 (1)根据平行四边形的性质可得到AB∥CD,从而可得到AB∥DF,根据平行线的性质可得到两组角相等,已知点E是BC的中点,从而可根据AAS来判定△BAE≌△CFE,根据全等三角形的对应边相等可证得AB=CF,进而得出CF=CD;
(2)利用全等三角形的判定与性质得出AE=EF,再利用角平分线的性质以及等角对等边求出DA=DF,利用等腰三角形的性质求出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
则在△BAE和△CFE中,
$\left\{\begin{array}{l}{∠BAE=∠CFE}\\{∠ECF=∠EBA}\\{BE=CE}\end{array}\right.$,
∴△BAE≌△CFE(AAS),
∴AB=CF,
∴CF=CD;
(2)解:DE⊥AF,
理由:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
又由(1)知△BAE≌△CFE,
∴AE=EF,
∴DE⊥AF.
点评 此题主要考查学生对平行四边形的性质以及全等三角形的判定与性质,证明线段相等的常用方法是证明三角形全等.

练习册系列答案
相关题目
12.当0<x<1时,x,$\frac{1}{x}$,x2的大小顺序是( )
| A. | $\frac{1}{x}$<x<x2 | B. | x<x2<$\frac{1}{x}$ | C. | x2<x<$\frac{1}{x}$ | D. | $\frac{1}{x}$<x2<x |
10.x的值不小于-2,用不等式表示x的范围是( )
| A. | x>-2 | B. | x<-2 | C. | x≥-2 | D. | x≤-2 |
7.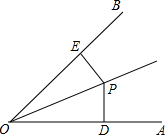 如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
 如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
11.某地冬季一周的气温走势如下表所示,那么这一周的平均气温为2℃.
| 温度 | -1℃ | 1℃ | 2℃ | 3℃ | 4℃ |
| 天数 | 1 | 2 | 1 | 1 | 2 |
 一次函数y1=3x+4和函数y2=2x+1的图象如图所示,解答下列问题:
一次函数y1=3x+4和函数y2=2x+1的图象如图所示,解答下列问题: 如图所示,O是直线AB上任一点,OC为过O点的射线,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
如图所示,O是直线AB上任一点,OC为过O点的射线,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.