题目内容
19.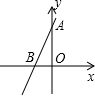 如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )| A. | x<-2 | B. | -2<x<-1 | C. | -2<x<0 | D. | -1<x<0 |
分析 求不等式0<kx+b<4的解集,就是求函数值在0到4之间所对应的自变量的范围,然后根据图象解决问题.
解答 解:当-2<x<0时,0<kx+b<4.
故选C.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
10.x的值不小于-2,用不等式表示x的范围是( )
| A. | x>-2 | B. | x<-2 | C. | x≥-2 | D. | x≤-2 |
7.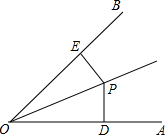 如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
 如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
4.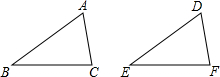 如图所示的△ABC和△DEF,给出下列三组条件:
如图所示的△ABC和△DEF,给出下列三组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
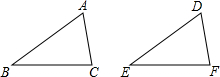 如图所示的△ABC和△DEF,给出下列三组条件:
如图所示的△ABC和△DEF,给出下列三组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 0组 |
11.某地冬季一周的气温走势如下表所示,那么这一周的平均气温为2℃.
| 温度 | -1℃ | 1℃ | 2℃ | 3℃ | 4℃ |
| 天数 | 1 | 2 | 1 | 1 | 2 |
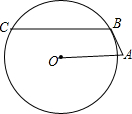 如图,AB切⊙O于点B,OA=2$\sqrt{3}$,∠BAO=60°,弦BC∥OA,则$\widehat{BC}$的长为2π(结果保留π).
如图,AB切⊙O于点B,OA=2$\sqrt{3}$,∠BAO=60°,弦BC∥OA,则$\widehat{BC}$的长为2π(结果保留π). 一次函数y1=3x+4和函数y2=2x+1的图象如图所示,解答下列问题:
一次函数y1=3x+4和函数y2=2x+1的图象如图所示,解答下列问题: 如图,数轴上有A、B、C、D四点,根据图中各点的位置,判断与10-2$\sqrt{39}$最接近的点是( )
如图,数轴上有A、B、C、D四点,根据图中各点的位置,判断与10-2$\sqrt{39}$最接近的点是( )