题目内容
10.已知关于x的分式方程$\frac{1-m}{x-1}$-1=$\frac{2}{1-x}$的解是正数,则m的取值范围是( )| A. | m<4且m≠3 | B. | m<4 | C. | m≤4且m≠3 | D. | m>5且m≠6 |
分析 先利用m表示出x的值,再由x为正数求出m的取值范围即可.
解答 解:方程两边同时乘以x-1得,1-m-(x-1)+2=0,
解得x=4-m.
∵x为正数,
∴4-m>0,解得m<4.
∵x≠1,
∴4-m≠1,即m≠3.
∴m的取值范围是m<4且m≠3.
故选A.
点评 本题考查的是分式方程的解,熟知求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值,这个值叫方程的解是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.若$\frac{4a}{4-|a|}$有意义,则$\frac{4a}{4-a}$的值( )
| A. | 无意义 | B. | 有意义 | C. | 值为0 | D. | 以上答案都不对 |
5.将235000000用科学记数法表示为( )
| A. | 235×106 | B. | 2.35×107 | C. | 2.35×108 | D. | 0.235×109 |
19.如果在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式正确的是( )
| A. | tanB=$\frac{2}{3}$ | B. | cotB=$\frac{2}{3}$ | C. | sinB=$\frac{2}{3}$ | D. | cosB=$\frac{2}{3}$ |
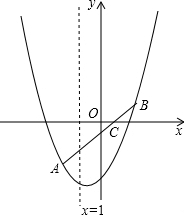 如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.
如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.