题目内容
20.(1)$\left\{\begin{array}{l}{y=2x-3}\\{5x+y=11}\end{array}\right.$; (2)$\left\{\begin{array}{l}{x+3y=-1}\\{3x-y=7}\end{array}\right.$.分析 (1)利用代入消元法解出方程组;
(2)利用加减消元法解出方程组.
解答 解:(1)$\left\{\begin{array}{l}{y=2x-3①}\\{5x+y=11②}\end{array}\right.$,
把①代入②得,5x+2x-3=11,
解得,x=2,
把x=2代入①得,y=1,
则方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+3y=-1①}\\{3x-y=7②}\end{array}\right.$,
①+②×3得,10x=20,
解得,x=2,
把x=2代入①得,y=-1,
则方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解法,掌握代入消元法和加减消元法解二元一次方程组的一般步骤是解题的关键.

练习册系列答案
相关题目
8.已知直角三角形的两边长分别为6和8,则这个直角三角形的周长是( )
| A. | 24或14+2$\sqrt{7}$ | B. | 24 | C. | 20或14-2$\sqrt{7}$ | D. | 22或14+2$\sqrt{7}$ |
10.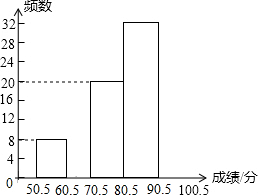 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
(1)求a的值,并补全频数分布直方图.
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
 某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:
某中学组织了一次“中华民族的伟大复兴”历史知识竞赛,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频率分布直方图如下:| 分组 | 频数 | 频率 |
| 50.5-60.5 | 8 | 0.08 |
| 60.5-70.5 | 12 | 0.12 |
| 70.5-80.5 | 20 | 0.2 |
| 80.5-90.5 | 32 | 0.32 |
| 90.5-100.5 | 28 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
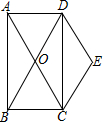 如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.