题目内容
14.下列各组数是三角形的三边,能组成直角三角形的一组数是( )| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 3,4,5 | D. | 6,8,12 |
分析 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形,据此判断即可.
解答 解:(A)∵$(\sqrt{3})^{2}+(\sqrt{4})^{2}≠(\sqrt{5})^{2}$,以$\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$为三边的三角形不是直角三角形,故(A)错误;
(B)∵22+32≠42,以2、3、4为三边的三角形不是直角三角形,故(B)错误;
(C)∵32+42=52,以3、4、5为三边的三角形是直角三角形,故(C)正确;
(D∵62+82≠122,以6、8、12为三边的三角形不是直角三角形,故(D)错误;
故选(C)
点评 本题主要考查了勾股定理的逆定理,勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形,必须满足较小两边平方的和等于最大边的平方才能做出判断.

练习册系列答案
相关题目
4.$\left\{\begin{array}{l}{0.2x-0.3y=2}\\{0.2x-0.7y=-1.5}\end{array}\right.$最适合用的方法是( )
| A. | 换元法 | B. | 加减消元法 | C. | 代入消元法 | D. | 无法确定 |
3.一个直角三角形的斜边长比一条直角边长多2cm,另一条直角边长6cm,那么这个直角三角形的斜边长为( )
| A. | 4cm | B. | 8cm | C. | 10cm | D. | 12cm |
4.下列命题中,是假命题的是( )
| A. | 等角的余角相等 | B. | 若a>b,且m≠0,则am>bm | ||
| C. | 三角形的外角和等于360° | D. | 两直线平行,同位角相等 |

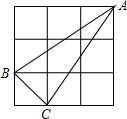 如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则△ABC的面积为$\frac{5}{2}$.
如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则△ABC的面积为$\frac{5}{2}$. 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).