题目内容
13.如图①,△ABC的两条平分线AD、BE相交于点P,若∠C=70°,求∠APB的度数.如图②,P是△ABC内一点,且PA平分∠CAB,PB平分∠CBA,求证:∠APB=90°+$\frac{1}{2}$∠C.

分析 (1)先根据直角三角形的性质求出∠CAB+∠ABC的度数,再根据角平分线的定义得出∠PAB+∠ABP的度数,由三角形内角和定理即可得出结论;
(2)根据角平分线的定义和三角形的内角和定理求出∠CAB+∠CBA的值,再利用三角形的内角和定理求出∠APB的值.
解答 解:(1)∵在△ABC中,∠C=70°,
∴∠CAB+∠ABC=110°,
∵∠A、∠B的平分线相交于点P,
∴∠PAB+∠ABP=$\frac{1}{2}$(∠CAB+∠ABC)=$\frac{1}{2}$×110°=55°,
∴∠APB=180°-(∠PAB+∠ABP)=180°-55°=125°;
(2)∵PA平分∠CAB,PB平分∠CBA,
∴∠PAB=∠PAC=$\frac{1}{2}$∠CAB,∠CPB=∠ABP=$\frac{1}{2}$∠CBA,
∴∠PAB+∠PBA=$\frac{1}{2}$(∠CAB+∠CBA)=$\frac{180°-∠C}{2}$,
∴在△APB中,
∵∠PAB+∠PBA+∠APB=180°
∴∠APB=180°-(∠PAB+∠PBA)=180°-$\frac{180°-∠C}{2}$=$\frac{1}{2}$∠ACB+90°.
点评 本题考查的是三角形内角和定理及角平分线的定义,熟知三角形的内角和是180°是解答此题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
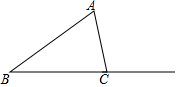 在证明三角形内角和定理时,小明的想法是把三个角凑到C处,他过点C作直线CD∥AB,请你按照他的想法在图中作出直线CD.
在证明三角形内角和定理时,小明的想法是把三个角凑到C处,他过点C作直线CD∥AB,请你按照他的想法在图中作出直线CD. 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,试求出正方形ADEF的边长.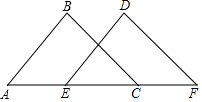 如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:∠B=∠D.
如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:∠B=∠D.