题目内容
10.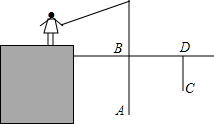 星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?
星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?
分析 根据题意直接得出AE,EC的长,再利用勾股定理得出AC的长,进而求出答案.
解答  解:如图所示:过点C作CE⊥AB于点E,连接AC,
解:如图所示:过点C作CE⊥AB于点E,连接AC,
由题意可得:EC=BD=1.2m,AE=AB-BE=AB-DC=1.3-0.8=0.5(m),
故AC=$\sqrt{E{C}^{2}+A{E}^{2}}$=$\sqrt{1.{2}^{2}+0.{5}^{2}}$=1.3(m),
则1.3÷0.2=6.5(s),
答:这条鱼至少6.5秒后才能到这鱼饵处.
点评 此题主要考查了勾股定理的应用,根据题意得出AE,EC的长是解题关键.

练习册系列答案
相关题目
1.已知扇形的圆心角为150°,它所对应的弧长为20πcm,则此扇形的面积是( )
| A. | 24cm2 | B. | 48cm2 | C. | 240πcm2 | D. | 240cm2 |
18.当x为任意实数时,下列一定有意义的分式是( )
| A. | $\frac{{x}^{2}+1}{{x}^{2}}$ | B. | $\frac{x-1}{{x}^{2}-1}$ | C. | $\frac{x+1}{{x}^{2}+1}$ | D. | $\frac{x-1}{x+1}$ |
5.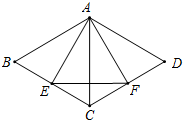 如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
 如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.抛物线y=x2-2x与坐标轴的交点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.计算的x3×x2结果是( )
| A. | x6 | B. | 6x | C. | x5 | D. | 5x |
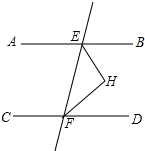 如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.
如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形. 如图,△ABC中AD是∠BAC的平分线,E、F分别是AB、BC上的点,且∠EDF+∠BAC=180°,求证:DE=DF.
如图,△ABC中AD是∠BAC的平分线,E、F分别是AB、BC上的点,且∠EDF+∠BAC=180°,求证:DE=DF.