题目内容
1. 如图,△ABC中AD是∠BAC的平分线,E、F分别是AB、BC上的点,且∠EDF+∠BAC=180°,求证:DE=DF.
如图,△ABC中AD是∠BAC的平分线,E、F分别是AB、BC上的点,且∠EDF+∠BAC=180°,求证:DE=DF.
分析 在AB上截取AG=AF,先证明△AGD≌△AFD,得出∠AGD=∠AFD,DG=DF;再根据角的关系求出∠4=∠3,证出DE=DG,即可得出结论DE=DF.
解答 证明:在AB上截取AG=AF,连接DG,如图所示: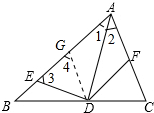 ∵AD是∠BAC的平分线,
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△ADG与△ADF中,$\left\{\begin{array}{l}{AG=AF}&{\;}\\{∠1=∠2}&{\;}\\{AD=AD}&{\;}\end{array}\right.$,
∴△AGD≌△AFD(SAS)
∴∠AGD=∠AFD,DG=DF
又∵∠AED+∠EDF+∠DFA+∠FAE=360°,∠EAF+∠EDF=180°,
∴∠AED+∠AFD=180°,
又∠4+∠AGD=180°,
∴∠4=∠3,
∴DE=DG,
∴DE=DF.
点评 本题考查了全等三角形的判定与性质、角的平分线的定义、等腰三角形的判定与性质;证明三角形全等和等腰三角形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.一个饲养场里的鸡的只数与猪的头数之和是70,鸡、猪的腿数之和是196,设鸡的只数是x,依题意列方程为( )
| A. | 2x+4(70-x)=196 | B. | 2x+4×70=196 | C. | 4x+2(70-x)=196 | D. | 4x+2×70=196 |
13.使函数y=$\sqrt{4-2x}$有意义的自变量x的取值范围是( )
| A. | x≤2 | B. | x≠2 | C. | x≥2 | D. | x<2 |
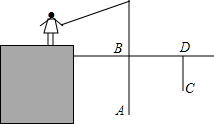 星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?
星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?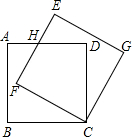 如图所示,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,
如图所示,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG, 如图所示,在△ABC中,D,E,F分别是AB,AC,BC边的中点,且AB=10,BC=4,AC=8,则△DEF的周长为11.
如图所示,在△ABC中,D,E,F分别是AB,AC,BC边的中点,且AB=10,BC=4,AC=8,则△DEF的周长为11.