题目内容
16.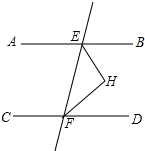 如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.
如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.
分析 由平行线的性质和角平分线的定义可求得∠HEF+∠HFE=90°,可判定△EFH为直角三角形.
解答 证明:
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EH平分∠BEF,FH平分∠EFD,
∴∠BEF=2∠HEF,∠EFD=2∠HFE,
∴2∠HEF+2∠HFE=180°,
∴∠HEF+∠HFE=90°,
∴∠EHF=90°,
∴△EFH为直角三角形.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
3.如图,已知∠MON,在∠MON内逐一画射线,下面三个图中分别有3个、6个、10个角(不大于平角的角).当∠MON内有n条射线时,角的个数为( )
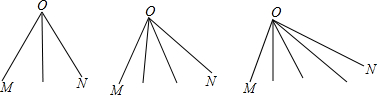

| A. | $\frac{{n}^{2}}{2}$ | B. | $\frac{n(n+1)}{2}$ | C. | $\frac{n(n-1)}{2}$ | D. | $\frac{(n+1)(n+2)}{2}$ |
1.已知等腰△ABC中,AD⊥BC于点D,且AD=$\frac{1}{2}$BC,则△ABC底角的度数为( )
| A. | 45° | B. | 75° | C. | 45°或15°或75° | D. | 60° |
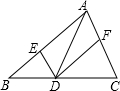 如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,下列说法:(1)四边形AEDF是平行四边形;(2)若∠BAC=90°,则四边形AEDF是矩形;(3)若AD平分∠BAC,则四边形AEDF是菱形;(4)若AD⊥BC且AB=AC,则四边形AEDF是正方形.其中正确的是(1)(2)(3).(只填正确答案的序号).
如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,下列说法:(1)四边形AEDF是平行四边形;(2)若∠BAC=90°,则四边形AEDF是矩形;(3)若AD平分∠BAC,则四边形AEDF是菱形;(4)若AD⊥BC且AB=AC,则四边形AEDF是正方形.其中正确的是(1)(2)(3).(只填正确答案的序号).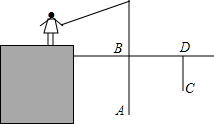 星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?
星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处? 如图所示,在△ABC中,D,E,F分别是AB,AC,BC边的中点,且AB=10,BC=4,AC=8,则△DEF的周长为11.
如图所示,在△ABC中,D,E,F分别是AB,AC,BC边的中点,且AB=10,BC=4,AC=8,则△DEF的周长为11.