题目内容
20.已知关于x,y的方程组$\left\{\begin{array}{l}x+3y=4-a\\ x-y=3a\end{array}\right.$,其中-3≤a≤1,给出下列结论:①$\left\{\begin{array}{l}x=5\\ y=-1\end{array}\right.$是方程组的解;②当a=-2时,x,y的值互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解.其中正确的是②③.分析 将a看做已知数表示出方程组的解,即可做出判断.
解答 解:方程组$\left\{\begin{array}{l}{x+3y=4-a①}\\{x-y=3a②}\end{array}\right.$,
①-②得:4y=4-4a,即y=1-a,
①+②×3得:4x=8a+4,即x=2a+1,
当a=2时,x=5,y=-1,但是不满足-3≤a≤1,选项①错误;
当a=-2时,x=-3,y=3,x,y的值互为相反数,选项②正确;
当a=1时,x=3,y=0,方程为x+y=3,
把x=3,y=0代入方程得:左边=3+0=3=右边,选项③正确;
则正确的选项有②③,
故答案为:②③.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目

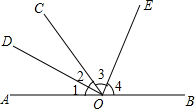 如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,OD⊥OE,垂足为点O.
如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,OD⊥OE,垂足为点O.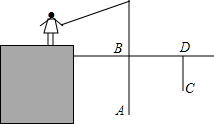 星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?
星期天小明去钓鱼,鱼钩A在离水面BD1.3米处,在距离鱼线1.2米处D点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2m/s的速度向鱼饵游来,那么这条鱼至少几秒后才能到这鱼饵处?