题目内容
9.如果三角形的两边长分别为3和6,第三边长是奇数,则第三边长可以是( )| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
分析 已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;又知道第三边长为奇数,就可以得出第三边的长度.
解答 解:设第三边的长为x,根据三角形的三边关系,
得6-3<x<6+3,即3<x<9,
又∵第三边长是奇数,
∴x=5或7.
故选C.
点评 本题主要考查了求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式组,然后解不等式组即可,难度适中.

练习册系列答案
相关题目
17.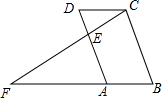 如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
 如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | ∠AEF=∠DEC | B. | BC:DE=CF:CE | C. | FA:AB=FE:EC | D. | FA:CD=AD:DE |
4. 如图,a∥b,∠1=150°,则∠2等于( )
如图,a∥b,∠1=150°,则∠2等于( )
 如图,a∥b,∠1=150°,则∠2等于( )
如图,a∥b,∠1=150°,则∠2等于( )| A. | 30° | B. | 90° | C. | 60° | D. | 50° |
14.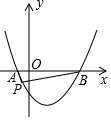 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )| A. | -1<m<0 | B. | -1<m<0或3<m<4 | C. | 0<m<3或m>4 | D. | m<-1或0<m<3 |
19.一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 不可能事件 | D. | 以上都不是 |
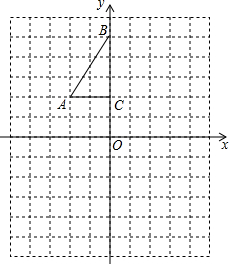 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).