题目内容
5.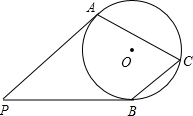 如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )
如图,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上,且$\widehat{ACB}$是优弧,则∠ACB等于( )| A. | 180°-2∠P | B. | 180°-∠P | C. | 90°-$\frac{1}{2}$∠P | D. | ∠P |
分析 连接OA、OB,由切线的性质结合四边形内角和可用∠P表示出∠AOB,再由圆周角定理可表示出∠ACB,可求得答案.
解答  解:
解:
如图,连接OA、OB,
∵PA、PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=180°-∠P,
∴∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$(180°-∠P)=90°-$\frac{1}{2}$∠P,
故选C.
点评 本题主要考查切线的性质,用∠P表示出∠AOB是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.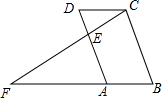 如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
 如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | ∠AEF=∠DEC | B. | BC:DE=CF:CE | C. | FA:AB=FE:EC | D. | FA:CD=AD:DE |
14.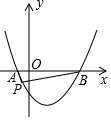 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )| A. | -1<m<0 | B. | -1<m<0或3<m<4 | C. | 0<m<3或m>4 | D. | m<-1或0<m<3 |
15. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )| A. | 48° | B. | 42° | C. | 40° | D. | 45° |