题目内容
1．
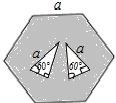如图，边长为a的正六边形内有两个三角形（数据如图），则$\frac{{S}_{空白}}{{S}_{阴影}}$=$\frac{1}{5}$．
分析 先求出正六边形的面积，再求出阴影部分面积、空白部分面积即可．
解答 解：∵S正六边形=6×$\frac{\sqrt{3}}{4}$•a2=$\frac{3\sqrt{3}}{2}$a2，S空白=2×$\frac{1}{2}$•$\frac{1}{2}$•a•$\frac{\sqrt{3}}{2}$•a=$\frac{\sqrt{3}}{4}$a2，
∴S阴=$\frac{5\sqrt{3}}{4}$a2，
∴$\frac{{S}_{空白}}{{S}_{阴影}}$=$\frac{1}{5}$．
故答案为$\frac{1}{5}$．
点评 本题考查正多边形与圆的有关知识、三角形的面积公式、直角三角形30度角的性质，记住等边三角形的面积=$\frac{\sqrt{3}}{4}$a2（a是等边三角形边长），解题的关键是理解正六边形是由6个等边三角形构成的，属于中考常考题型．
练习册系列答案
相关题目
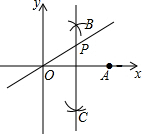如图，在平面直角坐标系中，O为原点，点A的坐标为（4，0），分别以点O、A为圆心，大于OA一半的长为半径作圆弧，两弧交于点B、C，直线BC与直线y=$\frac{3}{4}$x交于点P，则点P的坐标为（2，$\frac{3}{2}$）．
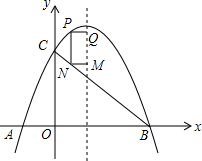如图，平面直角坐标系中，抛物线y=ax2+bx+2与x轴分别交于点A（-1，0）、B（3，0），与y轴交于点C，连结BC．点P是BC上方抛物线上一点，过点P作y轴的平行线，交BC于点N，分别过P、N两点作x轴的平行线，交抛物线的对称轴于点Q、M，设P点的横坐标为m．
9．下列等式成立的是（ ）
| A． | （a+4）（a-4）=a2-4 | B． | 2a2-3a=-a | C． | a6÷a3=a2 | D． | （a2）3=a6 |
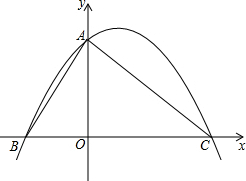将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B（-3，0）．
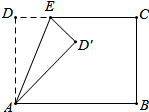如图，在矩形ABCD中，AD=5，AB=8，点E为DC边上的一个动点，把△ADE沿AE折叠，当点D的对应点刚好D落在矩形ABCD的对称轴上时，则DE的长为$\frac{5}{2}$或$\frac{5\sqrt{3}}{3}$．
13．若m＞n，下列不等式一定成立的是（ ）
| A． | m-2＞n+2 | B． | 2m＞2n | C． | -$\frac{m}{2}$＞$\frac{n}{2}$ | D． | m2＞n2 |
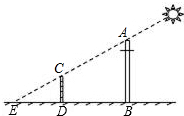小亮希望测量出电线杆AB的高度，他在电线杆旁的点D处立一标杆，标杆的影子DE与电线杆的影子BE部分重叠（即点E、C、A在一直线上），量得DB=2ED米，CD=1.5米．则电线杆AB的高为4.5米．