题目内容
16.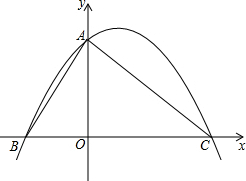 将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).(1)求该抛物线的解析式.
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标.
分析 (1)算出A、B、C三点坐标,由待定系数法直接求出抛物线解析式;
(2)设出P点坐标,根据PE∥AB得出△CEP∽△CAB,利用面积比等于相似比的平方得出三角形CEP的面积表达式,再用m表示出三角形APC的面积,三角形APC的面积减去三角形CEP的面积就是三角形APE的面积,再利用配方法求面积最大值以及P点坐标.
解答 解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过点A(0,6),
∴c=6,
∵抛物线的图象经过点点(-3,0)和(6,0),
∴$\left\{\begin{array}{l}{0=9a-3b+6}\\{0=36a+6a+6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=1}\end{array}\right.$,
∴抛物线的解析式为:$y=-\frac{1}{3}{x}^{2}+x+6$,
(2)设点P的坐标为(m,0),
则PC=6-m,${S}_{△ABC}=\frac{1}{2}BC•AO=\frac{1}{2}×9×6=27$,
∵PE∥AB,
∴△CEP∽△CAB,
$\frac{{S}_{△CEP}}{{S}_{△CAB}}=(\frac{PC}{BC})^{2}$,即:$\frac{{S}_{△CEP}}{27}=(\frac{6-m}{9})^{2}$,
∴${S}_{△CEP}=\frac{1}{3}(6-m)^{2}$,
∵${S}_{△APC}=\frac{1}{2}PC•AO=\frac{1}{2}(6-m)6$=3(6-m),
∴S△APE=S△APC-SCEP=$3(6-m)-\frac{1}{3}(6-m)^{2}$=$-\frac{1}{3}(m-\frac{3}{2})^{2}+\frac{27}{4}$,
当m=$\frac{3}{2}$时,S△APE有最大值为$\frac{27}{4}$,此时,P($\frac{3}{2}$,0).
点评 本题是二次函数综合题,主要考查了等腰直角三角形的性质、待定系数法求二次函数解析式、相似三角形的判定与性质、配方法求二次函数最值等知识点,难度不大,属中档题.利用相似三角形的面积比等于相似比的平方这一性质表示出三角形CEP的面积是解答第二问的关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案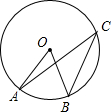 如图,点A、B、C在⊙O上,∠C+∠AOB=60°,则∠AOB的大小为( )
如图,点A、B、C在⊙O上,∠C+∠AOB=60°,则∠AOB的大小为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
 某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:
某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:| 组别 | 预习时间x(分钟) | 频数 |
| 1 | 0≤x<5 | 8 |
| 2 | 5≤x<10 | m |
| 3 | 10≤x<15 | 18 |
| 4 | 15≤x<20 | 13 |
| 合计 | 50 |
(1)统计表中m的值为11,并补全频数分布直方图;
(2)预习时间的中位数落在第3组;
(3)估计该校初一年级400名学生中,数学学科预习时间少于10分钟的学生人数.
| A. | -ab+1 | B. | -ab+b | C. | -a+1 | D. | -a-1 |
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{6}$ | D. | 6 |
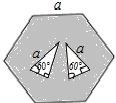 如图,边长为a的正六边形内有两个三角形(数据如图),则$\frac{{S}_{空白}}{{S}_{阴影}}$=$\frac{1}{5}$.
如图,边长为a的正六边形内有两个三角形(数据如图),则$\frac{{S}_{空白}}{{S}_{阴影}}$=$\frac{1}{5}$.