题目内容
2. 如图,Rt△ABC中,∠C=90°,BD=4,CD=2,∠ADB=3∠ABD,则AD=$\frac{8\sqrt{10}}{5}$.
如图,Rt△ABC中,∠C=90°,BD=4,CD=2,∠ADB=3∠ABD,则AD=$\frac{8\sqrt{10}}{5}$.
分析 如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,证明∠AED=∠ADE=2α,AE=AD;证明AE=2BE(设为2λ),得到AD=AE=2λ;利用勾股定理,可证明4λ2-4=9λ2-36,解得:λ=$\frac{4\sqrt{10}}{5}$,求出AD即可解决问题.
解答 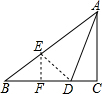 解:如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,设BE=λ,
解:如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,设BE=λ,
则BE=DE=λ,BF=DF=2,CF=4;
∴∠ABD=∠EDB=α;
∵∠AED=∠ABD+∠EDB=2α,∠ADB=3∠ABD=3α,
∴∠AED=∠ADE=2α,AE=AD;
∵EF⊥BC,AC⊥BC,
∴EF∥AC,$\frac{AE}{BE}$=$\frac{CF}{BF}$=2,
∴AE=2BE=2λ,
∴AD=AE=2λ;
由勾股定理得:
AC2=AD2-DC2=4λ2-4,
AC2=AB2-BC2=9λ2-36,
∴4λ2-4=9λ2-36,
解得:λ=$\frac{4\sqrt{10}}{5}$,
∴AD=$\frac{8\sqrt{10}}{5}$,
故答案为:$\frac{8\sqrt{10}}{5}$.
点评 本题主要考查了相似三角形的判定及其性质、勾股定理及其应用问题,解题的关键是作辅助线,构造相似三角形,运用相似三角形的判定及其性质来分析.

练习册系列答案
相关题目
17. 如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
 如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )| A. | 95 | B. | 65 | C. | 50 | D. | 40 |
14. 如图,AB∥DE,∠ABC=25°,∠BCD=75°,则∠CDE=( )
如图,AB∥DE,∠ABC=25°,∠BCD=75°,则∠CDE=( )
 如图,AB∥DE,∠ABC=25°,∠BCD=75°,则∠CDE=( )
如图,AB∥DE,∠ABC=25°,∠BCD=75°,则∠CDE=( )| A. | 100° | B. | 70° | C. | 60° | D. | 50° |
 如图,正△ABC的边长是2,点M是边AB上任意一点(可与A,B重合),作MD⊥BC于D,作DE⊥AC于E,作EN⊥AB于N,给出以下结论:①MN的最大值是$\frac{3}{2}$;②当M是AB的中点时,AN=$\frac{5}{8}$;③当M,N重合时,AN=$\frac{2}{3}$;④当△MBD≌△EAN时,AN=$\frac{1}{2}$,其中正确的结论有②③.
如图,正△ABC的边长是2,点M是边AB上任意一点(可与A,B重合),作MD⊥BC于D,作DE⊥AC于E,作EN⊥AB于N,给出以下结论:①MN的最大值是$\frac{3}{2}$;②当M是AB的中点时,AN=$\frac{5}{8}$;③当M,N重合时,AN=$\frac{2}{3}$;④当△MBD≌△EAN时,AN=$\frac{1}{2}$,其中正确的结论有②③.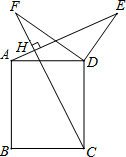 如图,四边形ABCD是矩形,点E和点F是矩形ABCD外两点,AE⊥CF于点H,AD=3,CD=4,DE=2.5,∠EDF=90°,则DF长是$\frac{10}{3}$.
如图,四边形ABCD是矩形,点E和点F是矩形ABCD外两点,AE⊥CF于点H,AD=3,CD=4,DE=2.5,∠EDF=90°,则DF长是$\frac{10}{3}$.