题目内容
17. 如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )| A. | 95 | B. | 65 | C. | 50 | D. | 40 |
分析 根据邻补角的概念求出∠AOF和∠AOC,根据角平分线的定义求出∠AOE,结合图形计算即可.
解答 解:∵∠BOF=140°,
∴∠AOF=180°-140°=40°,
∵∠BOC=130°,
∴∠AOC=50°,
∵OE是∠AOC的平分线,
∴∠AOE=$\frac{1}{2}$∠AOC=25°,
∴∠EOF=∠EOA+∠AOF=65°.
故选:B.
点评 本题考查的是对顶角和邻补角的概念和性质以及角平分线的定义,掌握邻补角之和等于180°是解题的关键.

练习册系列答案
相关题目
7. 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
5.一元二次方程x2-3x+3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
7.在△ABC中,画出边AC上的高,画法正确的是( )
| A. |  | B. |  | C. |  | D. |  |
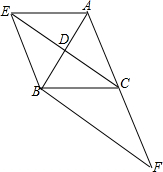 已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.
已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB. 如图,Rt△ABC中,∠C=90°,BD=4,CD=2,∠ADB=3∠ABD,则AD=$\frac{8\sqrt{10}}{5}$.
如图,Rt△ABC中,∠C=90°,BD=4,CD=2,∠ADB=3∠ABD,则AD=$\frac{8\sqrt{10}}{5}$.