题目内容
7.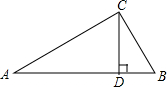 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长.
分析 先证明△BCD∽△BAC,利用相似比得到6:(9+BD)=BD:6,解方程可得BD=3,再在Rt△BCD中利用勾股定理计算出CD=3$\sqrt{3}$,然后在Rt△ACD中,利用正切的定义求tan∠ACD的值,利用勾股打开计算AC的长.
解答 解:∵CD⊥AB,
∴∠CDB=90°,
∵∠CBD=∠ABC,
∴△BCD∽△BAC,
∴BC:AB=BD:BC,即6:(9+BD)=BD:6,
∴BD=3,
在Rt△BCD中,CD=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
在Rt△ACD中,tan∠ACD=$\frac{AD}{CD}$=$\frac{9}{3\sqrt{3}}$=$\sqrt{3}$,
AC=$\sqrt{{9}^{2}+(3\sqrt{3})^{2}}$=6$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活运用勾股定理和锐角三角函数的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若y=(1+m)${x}^{{m}^{2}-7}$是二次函数,且开口向下,则m的值为( )
| A. | ±3 | B. | -3 | C. | +3 | D. | 0 |
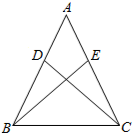 已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.
已知:如图,在△ABC中,AB=AC,在AB、AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.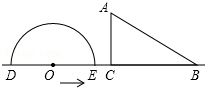 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧. 如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.
如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.
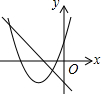
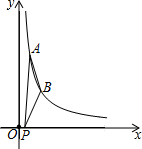 如图,双曲线$y=\frac{k}{x}$(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为6.
如图,双曲线$y=\frac{k}{x}$(x>0)经过点A(1,6)、点B(2,n),点P的坐标为(t,0),且-1≤t<3,则△PAB的最大面积为6. 如图,在Rt△ABC中,∠A=90°,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,连接CE,若AE=3,BE=5,则边AC的长为( )
如图,在Rt△ABC中,∠A=90°,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,连接CE,若AE=3,BE=5,则边AC的长为( )