题目内容
17. 如图,在Rt△ABC中,∠A=90°,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,连接CE,若AE=3,BE=5,则边AC的长为( )
如图,在Rt△ABC中,∠A=90°,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,连接CE,若AE=3,BE=5,则边AC的长为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
分析 由线段垂直平分线的性质得出CE=BE=5,由勾股定理求出AC即可.
解答 解:∵D是BC的中点,DE⊥BC,
∴CE=BE=5,
∵∠C=90°,
∴AC=$\sqrt{C{E}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
故选:B.
点评 本题考查了勾股定理、线段垂直平分线的性质;熟练掌握勾股定理,由线段垂直平分线的性质得出CE=BE是解决问题的关键.

练习册系列答案
相关题目
6.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.关于x的一元二次方程x2-5x+k=0有两个不相等的实数根,则k可取的最大整数为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
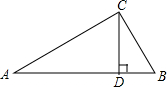 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长. 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米). 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE. 如图,AD是⊙O的直径,AB为⊙O的弦,BC与⊙O相切,B为切点,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O的弦,BC与⊙O相切,B为切点,OP与AB的延长线交于点P.点C在OP上,且BC=PC. 由若干相同的小正方体搭成的几何体的主视图与左视图如图所示,则该几何体最多由10个小正方体搭成.
由若干相同的小正方体搭成的几何体的主视图与左视图如图所示,则该几何体最多由10个小正方体搭成.