题目内容
15. 如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.
如图,A、B分别为数轴上两点,A点对应的数为-20,B点对应的数为80.(1)请写出与A、B两点距离相等的点M所对应的数;
(2)现有一只电子蚂蚁从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁恰好从A点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁恰好从A点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
分析 (1)设点M所对应的点为x,依据AM=BM列出方程并解答;
(2)先求出AB的长,再设t秒后相遇即可得出关于t的一元一次方程,求出t的值,可得出C点对应的数;
(3)先求出AB的长,再设t秒后相遇即可得出关于t的一元一次方程,求出t的值,可得出C点对应的数.
解答 解:(1)点M所对应的点为x,
依题意得:x-(-20)=80-x,
所以x+20=80-x,
解得x=30.
答:与A,B两点距离相等的点M所对应的数是30;
(2)∵A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为80,
∴AB=80+20=100,
设t秒后P、Q相遇,
∵电子蚂蚁从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁恰好从A点出发,以4单位/秒的速度向右运动,
∴6t+4t=100,解得t=10秒;
∴此时走过的路程=6×10=60,
∴此时C点表示的数为80-60=20.
答:C点对应的数是20.
(3)∵A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为80,
∴AB=80+20=100,
设t秒后P、Q相遇,
∵电子蚂蚁从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁恰好从A点出发,以4单位/秒的速度向右运动,
∴6t-4t=100,解得t=50秒;
∴此时走过的路程=6×50=300,
∴此时C点表示的数为80-300=-220.
答:C点对应的数是-220.
点评 本题考查了一元一次方程的应用,数轴.熟知数轴上两点间距离的定义是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
6. 如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
 如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列各对数中,互为相反数的是( )
| A. | 2和$\frac{1}{2}$ | B. | -0.5和$\frac{1}{2}$ | C. | -3和$\frac{1}{3}$ | D. | $\frac{1}{2}$和-2 |
 已知抛物线y=ax2+bx经过点A(-3、-3)和点P(t、0),且t≠0
已知抛物线y=ax2+bx经过点A(-3、-3)和点P(t、0),且t≠0 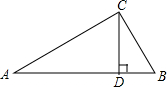 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长. 如图,⊙O的直径AB=10m,C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD、BD.
如图,⊙O的直径AB=10m,C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD、BD. 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.