题目内容
18.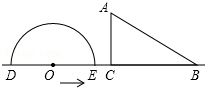 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧.(1)当△ABC的一边与半圆O相切时,请画出符合题意得图形.
(2)当△ABC的一边与半圆O相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,求重叠部分的面积.
分析 (1)因为点D,E始终在直线BC,所以当△ABC的一边与半圆O相切时只有三种情况,再分别画出即可;
(2)本题要分当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形分别计算即可.
解答 解:(1)如图所示: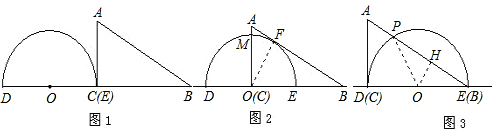
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.
①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:S扇形EOM=$\frac{1}{4}$π×62=9π(cm2)
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H.
则PH=BH.在Rt△OBH中,∠OBH=30°,OB=6cm
则OH=3cm,BH=3$\sqrt{3}$cm,BP=6$\sqrt{3}$cm,S△POB=$\frac{1}{2}$×6$\sqrt{3}$×3=9$\sqrt{3}$(cm2)
又因为∠DOP=2∠DBP=60°
所以S扇形DOP=6π(cm2)
所求重叠部分面积为:S△POB+S扇形DOP=9$\sqrt{3}$+6π(cm2),
综上可知当半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分则重叠部分的面积是9π或9$\sqrt{3}$+6π.
点评 此题主要考查了切线的性质、扇形的面积公式,直角三角形的面积公式,锐角三角函数的概念、根据直线与圆的位置关系画出符合题意的图形是解题的关键.

练习册系列答案
相关题目
6. 如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
 如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )
如图,P为正方形ABCD边BC的中点,DE⊥AP于点E,F为AP上一点,AE=EF,∠CDF的平分线交AP的延长线于点G,连接CG,下列结论:①DE=2AE;②AG⊥CG;③△DEG为等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列各对数中,互为相反数的是( )
| A. | 2和$\frac{1}{2}$ | B. | -0.5和$\frac{1}{2}$ | C. | -3和$\frac{1}{3}$ | D. | $\frac{1}{2}$和-2 |
 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,若原正方形空地边长是xm,则可列方程为(x-1)(x-3)=20.
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,若原正方形空地边长是xm,则可列方程为(x-1)(x-3)=20. 如图,点A、B、C都在⊙O上,若∠O=40°,则∠C=20度.
如图,点A、B、C都在⊙O上,若∠O=40°,则∠C=20度. 如图是由直角边长为a、b,斜边长为c的4个全等的直角三角形拼成的正方形.试利用这个图形来验证勾股定理.
如图是由直角边长为a、b,斜边长为c的4个全等的直角三角形拼成的正方形.试利用这个图形来验证勾股定理.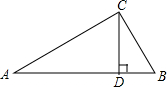 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长. 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).