题目内容
12.在同一直角坐标系中,函数y=mx+m和函数y=-mx2+2x+$\frac{3}{2}$(m是常数,且m≠0)的图象可能是( )| A. | 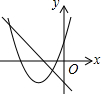 | B. | 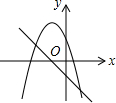 | C. | 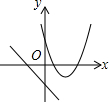 | D. | 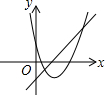 |
分析 首先确定m的正负,对于二次函数y=ax2+bx+c,当a>0时,开口向上;当a<0时,开口向下.对称轴为x=-$\frac{b}{2a}$,进而分析得出答案.
解答 解:A.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+$\frac{3}{2}$开口方向朝上,对称轴为x=-$\frac{b}{2a}$=$\frac{1}{m}$<0,则对称轴应在y轴右侧,故A选项正确;
B.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+$\frac{3}{2}$开口方向朝上,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+$\frac{3}{2}$开口方向朝上,对称轴为x=-$\frac{b}{2a}$=$\frac{1}{m}$<0,则对称轴应在y轴右侧,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m>0,即函数y=-mx2+2x+$\frac{3}{2}$开口方向朝下,与图象不符,故D选项错误.
故选:A.
点评 此题主要考查了一次函数和二次函数的图象性质以及分析能力和读图能力,要掌握它们的性质才能灵活解题.

练习册系列答案
相关题目
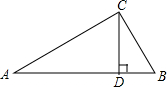 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AD=9,BC=6.求:tan∠ACD及AC的长. 如图,⊙O的直径AB=10m,C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD、BD.
如图,⊙O的直径AB=10m,C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD、BD. 由若干相同的小正方体搭成的几何体的主视图与左视图如图所示,则该几何体最多由10个小正方体搭成.
由若干相同的小正方体搭成的几何体的主视图与左视图如图所示,则该几何体最多由10个小正方体搭成.