题目内容
如图，在△ABG中，D、E和C、F分别是AG、BG的三等分点，则S△GDC ：SEFCD：SABEF=考点：相似三角形的判定与性质
专题：
分析：由在△ABG中，D、E和C、F分别是AG、BG的三等分点，可得CD∥EF∥AB，GC：GE：GA=1：2：3，即可证得△GCD∽△GEF∽△GAB，然后由相似三角形面积比等于相似比的平方，即可求得答案．
解答：解：∵在△ABG中，D、E和C、F分别是AG、BG的三等分点，
∴CD∥EF∥AB，GC：GE：GA=1：2：3，
∴△GCD∽△GEF∽△GAB，
∴S△GDC ：S△GEF：S△GAB=1：4：9，
∴S△GDC ：SEFCD：SABEF=1：3：5．
故答案为：1：3：5．
∴CD∥EF∥AB，GC：GE：GA=1：2：3，
∴△GCD∽△GEF∽△GAB，
∴S△GDC ：S△GEF：S△GAB=1：4：9，
∴S△GDC ：SEFCD：SABEF=1：3：5．
故答案为：1：3：5．
点评：此题考查了相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AB是⊙O的直径，AB=d，过A作⊙O的切线并在其上取一点C，使AC=AB，连接OC交⊙O于点D，BD的延长线交AC于E．
如图，△ABC是等腰三角形，AB=AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F．
如图，在平面直角坐标系中，点A，C分别在x轴，y轴上，四边形ABCO为矩形，AB=4，BC=3，点D与点A关于y轴对称，点E，F分别是线段AD，AC上的动点（点E不与点A，D重合），且∠CEF=∠ACB．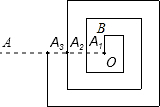
如图是一个回形图，其回形通道的宽和OB的长均为1，回形线与射线OA交于A1、A2、A3…若从O到点A1的回形线为第一圈（长为7），从点A1到A2为第二圈，…以此类推，则第10圈的线长为（ ）