题目内容
10.我们都知道$\sqrt{3}$是无理数,而无理数是无限不循环小数,因此$\sqrt{3}$的小数部分我们不可能全部写出来,但是因为1<$\sqrt{3}$<2,因此我们可以用1来表示它的整数部分,用$\sqrt{3}$-1表示它的小数部分,若$\sqrt{10}$的整数部分是a,$\sqrt{5}$的小数部分是b,则ab的值为( )| A. | 5$\sqrt{2}$ | B. | 3$\sqrt{5}$-6 | C. | 3$\sqrt{6}$-5 | D. | 2$\sqrt{10}$-6 |
分析 根据3$<\sqrt{10}<4$,可得a的值,根据2<$\sqrt{5}$<3,可得b的值,根据有理数的乘法,可得答案.
解答 解:∵3$<\sqrt{10}<4$,
∴a=3,
∵2$<\sqrt{5}$<3,
∴b=$\sqrt{5}$-2,
∴ab=3×($\sqrt{5}$-2)=3$\sqrt{5}$-6,
故选B.
点评 本题考查了估算无理数的大小,根据3$<\sqrt{10}<4$,可得a的值,根据2$<\sqrt{5}$<3,可得b的值是解题关键.

练习册系列答案
相关题目
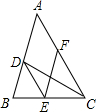 如图,CD是△ABC的角平分线,点E、F分别在BC、AC上,且DE∥AC,FE∥AB.
如图,CD是△ABC的角平分线,点E、F分别在BC、AC上,且DE∥AC,FE∥AB.