题目内容
15.已知2x+3y+z=0,x+y-z=0,求$\frac{{x}^{2}+{y}^{2}-{z}^{2}}{xy+xz-yz}$的值.分析 首先根据已知用z表示x,y,再将结果代入原式即可.
解答 解:∵2x+3y+z=0,x+y-z=0,
∴y=-3z,x=4z,
∴原式=$\frac{1{6z}^{2}+{9z}^{2}{-z}^{2}}{-1{2z}^{2}+{4z}^{2}+{3z}^{2}}$=$-\frac{24}{5}$.
点评 本题主要考查了代数式求值,用同一个字母表示另外两个是解答此题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | a4•a2=a8 | B. | a4+a2=a6 | C. | a2÷a-1=a3 | D. | (-2a3)2=-4a6 |
10.我们都知道$\sqrt{3}$是无理数,而无理数是无限不循环小数,因此$\sqrt{3}$的小数部分我们不可能全部写出来,但是因为1<$\sqrt{3}$<2,因此我们可以用1来表示它的整数部分,用$\sqrt{3}$-1表示它的小数部分,若$\sqrt{10}$的整数部分是a,$\sqrt{5}$的小数部分是b,则ab的值为( )
| A. | 5$\sqrt{2}$ | B. | 3$\sqrt{5}$-6 | C. | 3$\sqrt{6}$-5 | D. | 2$\sqrt{10}$-6 |
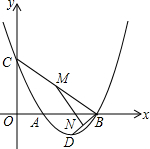 已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.
已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.