题目内容
1.(1)先分解因式,再求值:(m2+n2)2-4m2n2,其中m=-3,n=2.(2)解不等式组$\left\{\begin{array}{l}{-2x-1<5}\\{3x+6>0}\end{array}\right.$.
分析 (1)直接利用平方差公式分解因式,进而利用完全平方公式分解即可;
(2)分别解不等式,进而得出方程组的解.
解答 解:(1)(m2+n2)2-4m2n2
=(m2+n2)2-(2mn)2
=(m2+2mn+n2)(m2-2mn+n2)
=(m+n)2(m-n)2;
(2)$\left\{\begin{array}{l}{-2x-1<5①}\\{3x+6>0②}\end{array}\right.$,
解:由①得:x>-3,
由②得:x>-2,
故不等式组的解集为:x>-2.
点评 此题主要考查了公式法分解因式以及不等式组的解法,正确利用公式法分解因式是解题关键.

练习册系列答案
相关题目
9.在数据分析的过程中,有人对两个不同城市学生的数学成绩进行了分析,结果发现这两座城市统计的方差值都是10.34,那么下列说法中,正确的是( )
| A. | 两城市学生的成绩一样 | B. | 两城市学生的数学平均分一样 | ||
| C. | 两城市数学成绩的中位数一样 | D. | 两城市学生数学成绩波动情况一样 |
16.分式$\frac{{a}^{2}+a}{{a}^{2}+2a+1}$化简的结果是( )
| A. | $\frac{a}{a-1}$ | B. | $\frac{a+1}{a-1}$ | C. | $\frac{a}{a+1}$ | D. | a |
13.如果a>b,下列各式中不正确的是( )
| A. | a-4>b-4 | B. | -$\frac{a}{3}$<-$\frac{b}{3}$ | C. | -2a<-2b | D. | -5+a<-5+b |
10.我们都知道$\sqrt{3}$是无理数,而无理数是无限不循环小数,因此$\sqrt{3}$的小数部分我们不可能全部写出来,但是因为1<$\sqrt{3}$<2,因此我们可以用1来表示它的整数部分,用$\sqrt{3}$-1表示它的小数部分,若$\sqrt{10}$的整数部分是a,$\sqrt{5}$的小数部分是b,则ab的值为( )
| A. | 5$\sqrt{2}$ | B. | 3$\sqrt{5}$-6 | C. | 3$\sqrt{6}$-5 | D. | 2$\sqrt{10}$-6 |
 某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.
某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.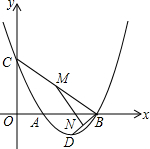 已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.
已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.