题目内容
5.解方程:$\frac{9}{{x}^{2}}$+$\frac{{x}^{2}}{4}$-2($\frac{3}{x}$+$\frac{x}{2}$)=0.分析 根据完全平方公式变形得出($\frac{3}{x}$+$\frac{x}{2}$)2-2($\frac{3}{x}$+$\frac{x}{2}$)-3=0,设$\frac{3}{x}$+$\frac{x}{2}$=y,则原方程化为y2-2y-3=0,求出y的值,再代入求出x即可.
解答 解:$\frac{9}{{x}^{2}}$+$\frac{{x}^{2}}{4}$-2($\frac{3}{x}$+$\frac{x}{2}$)=0,
($\frac{3}{x}$+$\frac{x}{2}$)2-2$•\frac{3}{x}$•$\frac{x}{2}$-2($\frac{3}{x}$+$\frac{x}{2}$)=0,
($\frac{3}{x}$+$\frac{x}{2}$)2-2($\frac{3}{x}$+$\frac{x}{2}$)-3=0,
设$\frac{3}{x}$+$\frac{x}{2}$=y,则原方程化为:y2-2y-3=0,
解得:y1=3,y2=-1,
当y=3时,$\frac{3}{x}$+$\frac{x}{2}$=3,
6+x2=6x,
x2-6x+6=0,
解得:x1=3+$\sqrt{3}$,x2=3-$\sqrt{3}$;
当y=-1时,$\frac{3}{x}$+$\frac{x}{2}$=-1,
x2+2x+6=0,此方程无解;
所以原方程的解为:x1=3+$\sqrt{3}$,x2=3-$\sqrt{3}$.
点评 本题考查了解分式方程的应用,能正确换元是解此题的关键,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.如果$\sqrt{2}$是a-1的相反数,那么a的值是( )
| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
16.分式$\frac{{a}^{2}+a}{{a}^{2}+2a+1}$化简的结果是( )
| A. | $\frac{a}{a-1}$ | B. | $\frac{a+1}{a-1}$ | C. | $\frac{a}{a+1}$ | D. | a |
13.如果a>b,下列各式中不正确的是( )
| A. | a-4>b-4 | B. | -$\frac{a}{3}$<-$\frac{b}{3}$ | C. | -2a<-2b | D. | -5+a<-5+b |
10.我们都知道$\sqrt{3}$是无理数,而无理数是无限不循环小数,因此$\sqrt{3}$的小数部分我们不可能全部写出来,但是因为1<$\sqrt{3}$<2,因此我们可以用1来表示它的整数部分,用$\sqrt{3}$-1表示它的小数部分,若$\sqrt{10}$的整数部分是a,$\sqrt{5}$的小数部分是b,则ab的值为( )
| A. | 5$\sqrt{2}$ | B. | 3$\sqrt{5}$-6 | C. | 3$\sqrt{6}$-5 | D. | 2$\sqrt{10}$-6 |
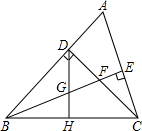 已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.