题目内容
10.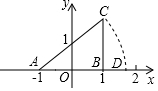 如图,Rt△ABC的边AB在x轴上,且A(-1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )
如图,Rt△ABC的边AB在x轴上,且A(-1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )| A. | ($\sqrt{2}$,0) | B. | (2$\sqrt{2}$,0) | C. | (2$\sqrt{2}$-1,0) | D. | (2$\sqrt{2}$-2,0) |
分析 由AB=2、∠BAC=45°知AC=AD=$\frac{AB}{cos∠BAC}$=2$\sqrt{2}$,根据OD=AD-AO=2$\sqrt{2}$-1可得答案.
解答 解:由题意知,AB=2、∠BAC=45°,
∴AC=AD=$\frac{AB}{cos∠BAC}$=$\frac{2}{\frac{\sqrt{2}}{2}}$=2$\sqrt{2}$,
则OD=AD-AO=2$\sqrt{2}$-1,
即点D的坐标为(2$\sqrt{2}$-1,0),
故选:C.
点评 本题主要考查坐标与图形的变化-旋转,掌握三角函数的定义和旋转的性质是解题的关键.

练习册系列答案
相关题目

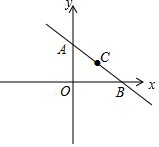 如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).
如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).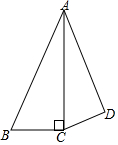 如图,AC是∠BAD的平分线,BC⊥AC,CD⊥AD.若AB=4,AD=$\frac{9}{4}$,则AC的长为3.
如图,AC是∠BAD的平分线,BC⊥AC,CD⊥AD.若AB=4,AD=$\frac{9}{4}$,则AC的长为3.