题目内容
已知
+
-
(
-
)=0,求x-
的值.
| x2 |
| 9 |
| 4 |
| x2 |
| 7 |
| 3 |
| x |
| 3 |
| 2 |
| x |
| 6 |
| x |
考点:换元法解分式方程
专题:
分析:根据换元法,可得一元二次方程,根据解一元二次方程,可得分式方程,根据解分式方程呢,可得答案.
解答:解:设u=(
-
),原方程等价于
u2-
u+
=0,去分母,得
3u2-7u+4=0.因式分解,得
(3u-4)(u-1)=0.
解得u=
,u=1.
当u=
时,(
-
)=
.
去分母,得x2-4x-6=0,解得x1=2+
,x2=2-
;
当u=1时,(
-
)=1,去分母,得x2-3x-6=0,解得x3=
,x4=
,
经检验:x1=2+
,x2=2-
,x3=
,x4=
是原分式方程的解,
当x1=2+
时,x-
=2+
-
=2+
-
=2+2
+2-
=4;
当x2=2-
时,x-
=2-
-
=2-
-
=2-
+2+
=4
当x3=
时,x-
=
-
=
-
=
-
=
+
=3;
当x4=
时,x-
=
-
=
-
=
-
=
+
=3+
;
综上所述:x-
=4,3,3+
.
| x |
| 3 |
| 2 |
| x |
u2-
| 7 |
| 3 |
| 4 |
| 3 |
3u2-7u+4=0.因式分解,得
(3u-4)(u-1)=0.
解得u=
| 4 |
| 3 |
当u=
| 4 |
| 3 |
| x |
| 3 |
| 2 |
| x |
| 4 |
| 3 |
去分母,得x2-4x-6=0,解得x1=2+
| 10 |
| 10 |
当u=1时,(
| x |
| 3 |
| 2 |
| x |
3+
| ||
| 2 |
3-
| ||
| 2 |
经检验:x1=2+
| 10 |
| 10 |
3+
| ||
| 2 |
3-
| ||
| 2 |
当x1=2+
| 10 |
| 6 |
| x |
| 10 |
| 6 | ||
2+
|
| 10 |
6(2-
| ||||
(2+
|
| 10 |
| 10 |
当x2=2-
| 10 |
| 6 |
| x |
| 10 |
| 6 | ||
2-
|
| 10 |
6(2+
| ||||
(2-
|
| 10 |
| 10 |
当x3=
3+
| ||
| 2 |
| 6 |
| x |
3+
| ||
| 2 |
| 6 | ||||
|
3+
| ||
| 2 |
| 12 | ||
3+
|
3+
| ||
| 2 |
12(3-
| ||||
(3+
|
3+
| ||
| 2 |
3-
| ||
| 2 |
当x4=
3-
| ||
| 2 |
| 6 |
| x |
3-
| ||
| 2 |
| 6 | ||||
|
3-
| ||
| 2 |
| 12 | ||
3-
|
3-
| ||
| 2 |
12(3+
| ||||
(3-
|
3+
| ||
| 2 |
3+
| ||
| 2 |
| 33 |
综上所述:x-
| 6 |
| x |
| 33 |
点评:本题考查了换元法解分式方程,利用了换元法解分式方程,解分式方程,解一元二次方程,代数式求值.

练习册系列答案
相关题目
 如图,把△ABC按逆时针转动一定的角度至△AB′C′,其中属于旋转角的是( )
如图,把△ABC按逆时针转动一定的角度至△AB′C′,其中属于旋转角的是( )| A、∠BAC |
| B、∠C′AB′ |
| C、∠BAB′ |
| D、∠BAC′ |
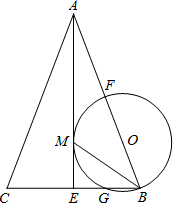 如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.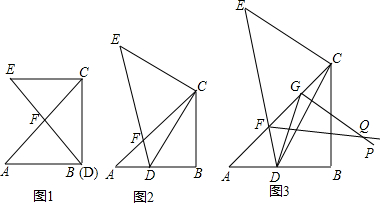
 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于