题目内容
作图并填空
如图,在Rt△ABC,∠BAC=90°,AD⊥BC于D,在②③图中,MN=AB,∠MNE=∠B,现要以②③图为基础,在射线NE上确定一点P,构造出一个△MNP与①图中某一个三角形全等.
(1)用边长限制P点,画法: ,可根据SAS,AAS,ASA,HL中的 得到.
(2)用直角限制点P,画法: ,可根据SAS,AAS,ASA,HL中的 得到 .
如图,在Rt△ABC,∠BAC=90°,AD⊥BC于D,在②③图中,MN=AB,∠MNE=∠B,现要以②③图为基础,在射线NE上确定一点P,构造出一个△MNP与①图中某一个三角形全等.

(1)用边长限制P点,画法:
(2)用直角限制点P,画法:
考点:全等三角形的判定与性质,作图—基本作图
专题:
分析:(1)作NP=BC,即可证明△MNP≌△ABC,即可解题;
(2)过M作MC⊥MN,即可证明△MNP≌△ABC,即可解题.
(2)过M作MC⊥MN,即可证明△MNP≌△ABC,即可解题.
解答:证明:(1)作NP=BC,
∵在△MNP和△ABC中,
,
∴△MNP≌△ABC,(SAS)
(2)过M作MC⊥MN,
∵在△MNP和△ABC中,
,
∴△MNP≌△ABC,(ASA)
故答案为:NP=BC,SAS,过M作MC⊥MN,ASA,△MNP≌△ABC.
∵在△MNP和△ABC中,
|
∴△MNP≌△ABC,(SAS)
(2)过M作MC⊥MN,
∵在△MNP和△ABC中,
|
∴△MNP≌△ABC,(ASA)
故答案为:NP=BC,SAS,过M作MC⊥MN,ASA,△MNP≌△ABC.
点评:本题考查了全等三角形的判定,本题属于开放题,熟练运用三角形全等判定方法是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于 如图所示,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.
如图所示,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,求BB′的长度.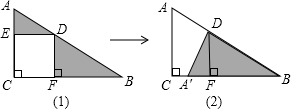 如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为
如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为