题目内容
 从△ABC的顶点A引三条线段:∠A的平分线AM,∠A的外角平分线AN,三角形外接圆的切线AK,点M、K、N依次排列在直线BC上,证明:MK=KN.
从△ABC的顶点A引三条线段:∠A的平分线AM,∠A的外角平分线AN,三角形外接圆的切线AK,点M、K、N依次排列在直线BC上,证明:MK=KN.考点:切线的性质
专题:证明题
分析:根据切线的性质得出∠CAK=∠B,由∠BAM=∠CAM,根据三角形外角的性质即可求得∠KAM=∠KMA,从而求得MK=AK,根据已知得出∠MAN=90°,从而得出∠KMA+∠N=90°,进而得出∠KAN=∠N,得出KN=AK,即可证得结论;
解答:解:∵AK是切线,
∴∠CAK=∠B,
∵AM是∠A的平分线,
∴∠BAM=∠CAM,
∴∠CAK+∠CAM=∠B+∠BAM,
即∠KAM=∠KMA,
∴MK=AK,
∵AM是∠A的平分线,AN是∠A的外角平分线,
∴∠MAN=90°,
∴∠KMA+∠N=90°,
∵∠KAM+∠KAN=∠MAN=90°,
∴∠KAN=∠N,
∴KN=AK,
∴MK=KN.
∴∠CAK=∠B,
∵AM是∠A的平分线,
∴∠BAM=∠CAM,
∴∠CAK+∠CAM=∠B+∠BAM,
即∠KAM=∠KMA,
∴MK=AK,
∵AM是∠A的平分线,AN是∠A的外角平分线,
∴∠MAN=90°,
∴∠KMA+∠N=90°,
∵∠KAM+∠KAN=∠MAN=90°,
∴∠KAN=∠N,
∴KN=AK,
∴MK=KN.
点评:本题考查了切线的性质,三角形外角的性质,等腰三角形的判定等,熟练掌握性质和定理是解题的关键.

练习册系列答案
相关题目
 如图,把△ABC按逆时针转动一定的角度至△AB′C′,其中属于旋转角的是( )
如图,把△ABC按逆时针转动一定的角度至△AB′C′,其中属于旋转角的是( )| A、∠BAC |
| B、∠C′AB′ |
| C、∠BAB′ |
| D、∠BAC′ |
 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处,(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于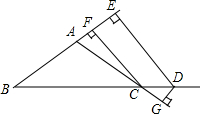 如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系.
如图,已知AB=AC,DE⊥BA的延长线于E,DG⊥AC的延长线于点G,CF⊥BC于点F,试探索DE和CF+DG的关系.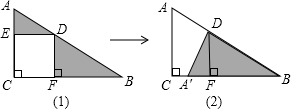 如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为
如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为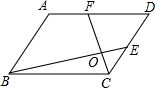 如图,平行四边形ABCD中,F为AD中点,CO=
如图,平行四边形ABCD中,F为AD中点,CO= 如图所示,AB,CD交于点O,且OC=45,OD=30,OB=36,当OA=
如图所示,AB,CD交于点O,且OC=45,OD=30,OB=36,当OA=