题目内容
1.在平面直角坐标系中,小明玩走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位,…,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第8步时,棋子所处位置的坐标是(9,2);当走完第2016步时,棋子所处位置的坐标是(2016,672).分析 设走完第n步时,棋子所处的位置为点Pn(n为自然数),根据走棋子的规律找出部分点Pn的坐标,根据坐标的变化找出变化规律“P3n+1(3n+1,n),P3n+2(3n+3,n),P3n+3(3n+3,n+1)”,依此规律即可得出结论.
解答 解:设走完第n步时,棋子所处的位置为点Pn(n为自然数),
观察,发现规律:P1(1,0),P2(3,0),P3(3,1),P4(4,1),…,
∴P3n+1(3n+1,n),P3n+2(3n+3,n),P3n+3(3n+3,n+1).
∵8=3×2+2,
∴P8(9,2).
∵2016=3×671+3,
∴P2016(2016,672).
故答案为:(9,2);(2016,672).
点评 本题考查了规律型中的点的坐标变化,解题的关键是找出变化规律“P3n+1(3n+1,n),P3n+2(3n+3,n),P3n+3(3n+3,n+1)”.本题属于中档题,难度不大,解决该题型题目时,根据点的变化找出变化规律是关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.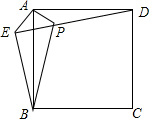 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{2}$;
③EB⊥ED;
④S正方形ABCD=4+$\sqrt{6}$;
⑤S△APD+S△APB=1+$\sqrt{6}$,
其中正确结论的序号是( )
 已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:
已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交ED于点P.若AE=AP=1,PB=$\sqrt{5}$.下列结论:①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{2}$;
③EB⊥ED;
④S正方形ABCD=4+$\sqrt{6}$;
⑤S△APD+S△APB=1+$\sqrt{6}$,
其中正确结论的序号是( )
| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
10.五一期间,绿化部门预在县城主要干道旁边种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵,求A、B两种花木的数量分别是多少棵?若设A,B花木各x棵,y棵,则有( )
| A. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y+600}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x+600}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=6600}\\{y=2x-600}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=6600}\\{x=2y-600}\end{array}\right.$ |
11. 如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )
如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )
 如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )
如图,直线a,b,c相交于点A,直线c,d,e相交于点B,则图中属于内错角的是( )| A. | ∠1和∠2 | B. | ∠2和∠3 | C. | ∠1和∠3 | D. | ∠3和∠4 |
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论: