题目内容
6.计算:($\frac{2}{\sqrt{2}+1}$+$\frac{2}{\sqrt{3}+\sqrt{2}}$+$\frac{2}{\sqrt{4}+\sqrt{3}}$+…+$\frac{2}{\sqrt{2017}+\sqrt{2016}}$)×($\sqrt{2017}$+1)分析 首先把每个式子分母有理化,合并同类二次根式,然后利用平方差公式即可求解.
解答 解:原式=[2($\sqrt{2}$-1)+2($\sqrt{3}$-$\sqrt{2}$)+2($\sqrt{4}$-$\sqrt{3}$)+…+2($\sqrt{2017}$-$\sqrt{2016}$)×($\sqrt{2017}$+1)
=2[$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2017}$-$\sqrt{2016}$)×($\sqrt{2017}$+1)
=2($\sqrt{2017}$-1)($\sqrt{2017}$+1)
=2(2017-1)
=4032.
点评 本题考查了二次根式的混合运算,正确对每个式子进行分母有理化是关键.

练习册系列答案
相关题目
16.方程x2+xy+y2=3(x+y)的整数解有( )
| A. | 3组 | B. | 4组 | C. | 5组 | D. | 6组 |
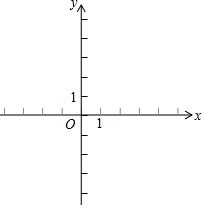 在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.
在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.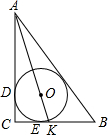 若⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点K,AC=4,CK=1,求内切圆的半径.
若⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点K,AC=4,CK=1,求内切圆的半径. 实数a,b在数轴上对应的点如图所示,请化简:|a+b|+|b-a|+|b|-|a-|a||
实数a,b在数轴上对应的点如图所示,请化简:|a+b|+|b-a|+|b|-|a-|a|| ;
;