题目内容
6.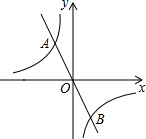 如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点
如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点(1)求双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x的表达式;
(2)当双曲线y=$\frac{{k}_{1}}{x}$的函数值为-3<y<-1时,请直接写出自变量x的取值范围.
分析 (1)把A(-1,m)、B(n,-2)分别代入双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x得$\left\{\begin{array}{l}{-m={k}_{1}}\\{-2n={k}_{1}}\\{m=-{k}_{2}}\\{-2=n{k}_{2}}\end{array}\right.$,解方程组即可得到结论;
(2)把y=-3,y=-1分别代入y=-$\frac{2}{x}$即可得到结论.
解答 解:(1)∵双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点,
∴$\left\{\begin{array}{l}{-m={k}_{1}}\\{-2n={k}_{1}}\\{m=-{k}_{2}}\\{-2=n{k}_{2}}\end{array}\right.$,
解得:k1=k2=±2,
∵k1<0,k2<0,
∴k1=k2=-2,
∴双曲线与直线的表达式分别为:y=-$\frac{2}{x}$,y=-2x;
(2)当y=-3时,x=$\frac{2}{3}$,当y=-1时,x=2,
∴双曲线y=$\frac{{k}_{1}}{x}$的函数值为-3<y<-1时,自变量x的取值范围为:$\frac{2}{3}$<x<2.
点评 本题考查了反比例函数和一次函数的交点问题,以及用待定系数法求反比例函数和一次函数的解析式,是基础知识要熟练掌握.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | a2+a3=a5 | B. | 3a2•2a3=6a6 | C. | (-a3)2=a6 | D. | (a-b)2=a2-b2 |
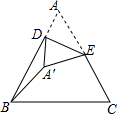 如图,△ABC中,AB=BC=AC=10,D是AB边上的动点,E是AC边的中点,将△ADE沿DE翻折得到△A′DE,连接BA′,则BA′的最小值是5$\sqrt{3}$-5.
如图,△ABC中,AB=BC=AC=10,D是AB边上的动点,E是AC边的中点,将△ADE沿DE翻折得到△A′DE,连接BA′,则BA′的最小值是5$\sqrt{3}$-5.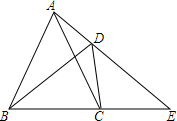 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.