题目内容
11.已知a+b=-3,ab=2,求$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值.解:$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{b}}{\sqrt{a}}$+$\frac{\sqrt{a}}{\sqrt{b}}$=$\frac{(\sqrt{b})^{2}+(\sqrt{a})^{2}}{\sqrt{a}•\sqrt{b}}$=$\frac{a+b}{\sqrt{ab}}$=$\frac{-3}{\sqrt{2}}$=-$\frac{3}{2}$$\sqrt{2}$.
我们知道$\sqrt{\frac{b}{a}}$≥0,$\sqrt{\frac{a}{b}}$≥0,其和必然不小于0,而题中的结果却是负数,说明计算过程有错,请你指出错在哪一步,错的原因是什么,正确解法又该怎样?
分析 根据有理数的加法和乘法法则,由a+b=-3,ab=2可知a<0,b<0,再根据二次根式的性质求解.
解答 解:$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$变形为$\frac{\sqrt{b}}{\sqrt{a}}$+$\frac{\sqrt{a}}{\sqrt{b}}$是错误的,
错的原因是由a+b=-3,ab=2可知a<0,b<0,则$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{-b}}{\sqrt{-a}}$+$\frac{\sqrt{-a}}{\sqrt{-b}}$,
正确的解法是:
$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{-b}}{\sqrt{-a}}$+$\frac{\sqrt{-a}}{\sqrt{-b}}$=$\frac{(\sqrt{-b})^{2}+(\sqrt{-a})^{2}}{\sqrt{-a}•\sqrt{-b}}$=$\frac{-(a+b)}{\sqrt{ab}}$=$\frac{3}{\sqrt{2}}$=$\frac{3}{2}$$\sqrt{2}$.
点评 考查了二次根式的应用,分母有理化,有理数的加法和乘法,解题的根据是由a+b=-3,ab=2得出a<0,b<0.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
3.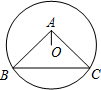 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
 如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.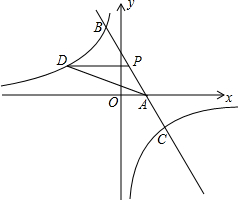 如图,已知一次函数y=-2x+3的图象与x轴交于点A,与反比例函数y=-$\frac{5}{x}$的图象交于B,C两点,点P是线段AB上的一个动点.
如图,已知一次函数y=-2x+3的图象与x轴交于点A,与反比例函数y=-$\frac{5}{x}$的图象交于B,C两点,点P是线段AB上的一个动点. 如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.
如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.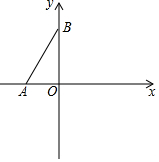 如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.
如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.