题目内容
1. 如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.(1)求DE的长;
(2)求△EDB的面积.
分析 (1)根据角平分线上的点到角的两边距离相等可得DE=CD;
(2)利用勾股定理列式求出AB的长度,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AE=AC,然后求出BE,再根据三角形面积公式列式计算即可得解.
解答 解:(1)∵∠C=90°,AD平分∠CAB,DE⊥AB,
∴DE=CD,
∵CD=3,
∴DE=3;
(2)∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=AB-AE=10-6=4,
∴△BDE的面积=$\frac{1}{2}$DE•BE=$\frac{1}{2}$×3×4=6.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,勾股定理,熟记各性质是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
12.∑表示数学中的求和符号,主要用于求多个数的和,∑下面的小字,i=1表示从1开始求和;上面的小字,如n表示求和到n为止.即$\sum_{i=1}^{n}$xi=x1+x2+x3+…+xn.则$\sum_{i=1}^{n}$(i2-i)表示( )
| A. | n2-1 | B. | 12+22+32+…+i2-i | ||
| C. | 12+22+32+…+n2-1 | D. | 12+22+32+…+n2-(1+2+3+…+n ) |
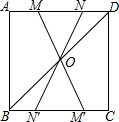 如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.
如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.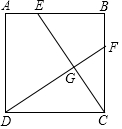 如图,正方形ABCD中,AE=BF.
如图,正方形ABCD中,AE=BF.