题目内容
6. 如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.
如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.
分析 由平行线的性质和角平分线定义证出∠ACF=∠AFC,得出AF=AC,同理:AC=CE,证出AF=CE=AC,得出四边形ACEF是平行四边形,即可证出四边形ACEF是菱形.
解答 证明:∵AB∥CD,
∴∠AFC=∠ECF,
∵CF平分∠ACD,
∴∠ECF=∠ACF,
∴∠ACF=∠AFC,
∴AF=AC,
同理:AC=CE,
∴AF=CE=AC,
又∵AF∥CE,
∴四边形ACEF是平行四边形,
∵AF=AC,
∴四边形ACEF是菱形.
点评 此题主要考查了平行四边形的性质以及菱形的判定,正确掌握菱形的判定方法是解题关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
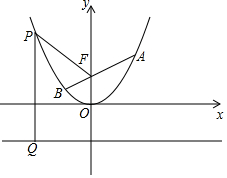 已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q
已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q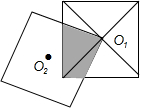 如图,已知两个边长为2的正方形,其中一个正方形的一个顶点与另一个正方形的中心O1重合,则重合部分的面积是多少?
如图,已知两个边长为2的正方形,其中一个正方形的一个顶点与另一个正方形的中心O1重合,则重合部分的面积是多少?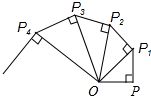 如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.
如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.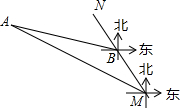 如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)
如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)