题目内容
8.已知函数y=3x-2(1)求函数图象与x轴、y轴的交点坐标.
(2)当x取什么值时,函数值是正数、零、负数?
(3)试判断点A(-2,-8)和B(1,3)是否在函数图象上?
分析 (1)分别计算出函数解析式中x=0时,y的值,以及y=0时,x的值即可;
(2)分别计算出y=0,y>0,y<0时,不等式和方程的解集;
(3)把A、B点代入解析式,满足解析式的就在此函数图象上,否则不在.
解答 解:(1)∵函数解析式y=3x-2中,当x=0时,y=-2,
∴与y轴的交点坐标为(0,-2),
∵当y=0时,x=$\frac{2}{3}$,
∴与x轴的交点坐标为($\frac{2}{3}$,0);
(2)当y=0时,x=$\frac{2}{3}$,
当y>0时,3x-2>0,
解得:x>$\frac{2}{3}$,
当y<0时,3x-2<0,
解得:x<$\frac{2}{3}$;
(3)把(-2,-8)代入y=3x-2中,3×(-2)-2=-8,则A在函数图象上;
把(1,3)代入y=3x-2中,3×1-2≠3,则B不在函数图象上.
点评 此题主要考查了一次函数图象上点的坐标特点,以及函数与方程、不等式的关系,关键是掌握一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20.已知正△ABC内接于圆O,四边形DEFG为半圆O的内接正方形(D,E在直径上,F,G在半圆上的正方形),S△ABC=a,S四边形DEFG=b,则$\frac{a}{b}$的值等于( )
| A. | 2 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3\sqrt{3}}{5}$ | D. | $\frac{15\sqrt{3}}{16}$ |
 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.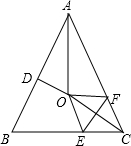 如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.
如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.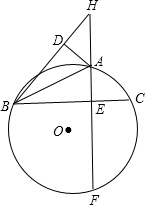 如图,△ABC内接于⊙O,AE和BD是它的两条高,相交于点H,直线AH交⊙O于点F,求证:EH=EF.
如图,△ABC内接于⊙O,AE和BD是它的两条高,相交于点H,直线AH交⊙O于点F,求证:EH=EF.