题目内容
2.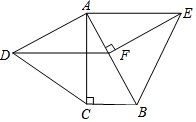 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE,过点E,作EF⊥AB,垂足为F,连结DF.求证:AE=DF.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE,过点E,作EF⊥AB,垂足为F,连结DF.求证:AE=DF.
分析 求出∠ABC=60°,根据等边三角形的性质得出等边三角形,∠DAC=∠BAE=∠FAE=60°,AB=AE,AC=AD,根据AAS推出Rt△ABC≌Rt△AEF,根据全等得出EF=AC=AD,求出∠DAB=∠AFE,推出AD∥EF,得到四边形ADFE是平行四边形,进而得到结论.
解答 证明:∵在Rt△ABC中,∠BAC=30°,
∴∠ABC=60°,
∵△ACD、△ABE是等边三角形,
∴∠DAC=∠BAE=∠FAE=60°,AB=AE,AC=AD,
∵EF⊥AB,即∠AFE=90°,
∴△AEF是直角三角形,
在Rt△ABC和Rt△AEF中,
$\left\{\begin{array}{l}{AE=AB}\\{∠FAE=∠ABC}\\{∠AFE=∠ACB}\end{array}\right.$,
∴Rt△ABC≌Rt△AEF(AAS),
∴EF=AC=AD,
∵∠DAB=∠DAC+∠CAB=60°+30°=90°,
∴∠DAB=∠AFE,
∴AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF.
点评 本题考查了平行四边形的性质和判定,等边三角形的性质,全等三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
7.若关于x的分式方程$\frac{3}{x-4}$+$\frac{x+m}{4-x}$=1有增根,则m的值是( )
| A. | m=0或m=3 | B. | m=3 | C. | m=0 | D. | m=-1 |
12.元旦联欢会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:
(1)猜想x、y之间的函数关系,并求出函数关系式.
(2)教室天花板对角线长10m,现需沿天花板对角线各拉一根彩纸链,则至少需要用多少个纸环?
| 纸环数x(个) | 1 | 2 | 3 | 4 | … |
| 彩纸链长度y( cm) | 19 | 36 | 53 | 70 | … |
(2)教室天花板对角线长10m,现需沿天花板对角线各拉一根彩纸链,则至少需要用多少个纸环?
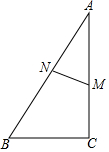 如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值. 如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°,1s后,火箭到达B点,此时测得仰角为45.5°,这枚火箭从点A到点B的平均速度是多少?(结果精确到0.01)
如图,一枚运载火箭从地面O处发射,当火箭到达A点时,从地面C处的雷达站测得AC的距离是6km,仰角是43°,1s后,火箭到达B点,此时测得仰角为45.5°,这枚火箭从点A到点B的平均速度是多少?(结果精确到0.01) 如图,AB是⊙O的直径,点C在⊙O上(异于A、B两点),AD⊥CD.
如图,AB是⊙O的直径,点C在⊙O上(异于A、B两点),AD⊥CD.