题目内容
11. 如图,AB是⊙O的直径,点C在⊙O上(异于A、B两点),AD⊥CD.
如图,AB是⊙O的直径,点C在⊙O上(异于A、B两点),AD⊥CD.①若BC=3,AB=5,求AC的长?
②若AC是∠DAB的平分线,求证:直线CD与⊙O相切.
分析 ①首先根据直径所对的圆周角为直角得到直角三角形,然后利用勾股定理求得AC的长即可;
②连接OC,证OC⊥CD即可;利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,即可得到OC∥AD,由于AD⊥CD,那么OC⊥CD,由此得证.
解答 解:①∵AB是⊙O的直径,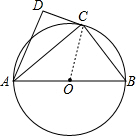
∴∠ACB=90°,
∵BC=3,AB=5,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
②证明:连接OC,
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠DAC=∠OCA,
∴AD∥OC,
又∵AD⊥DC,
∴∠ADC=90°,
∴∠OCD=90°,
∴DC是⊙O的切线.
点评 此题主要考查的是切线的判定方法.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
1.为考察小明和小亮的学习成绩,参看了他们上学期期中、期末成绩,如下表所示
根据你的观察小明的成绩较好.
| 成绩 姓名 | 期中 | 期末 |
| 小明 | 92 | 95 |
| 小亮 | 87 | 91 |
3.当-1≤x≤2时,二次函数y=x2+2mx+m+2,有最小值-3,则实数m的值为( )
| A. | $\frac{1+\sqrt{21}}{2}$或$\frac{1-\sqrt{21}}{2}$ | B. | 6或-$\frac{9}{5}$ | ||
| C. | 6或$\frac{1-\sqrt{21}}{2}$ | D. | 6或-$\frac{9}{5}$或$\frac{1-\sqrt{21}}{2}$或$\frac{1+\sqrt{21}}{2}$ |
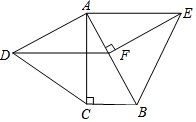 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE,过点E,作EF⊥AB,垂足为F,连结DF.求证:AE=DF.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,分别以直角边AC和斜边AB向外作等边△ACD、等边△ABE,过点E,作EF⊥AB,垂足为F,连结DF.求证:AE=DF.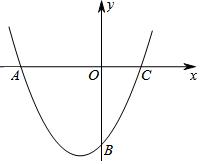 已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.