题目内容
8.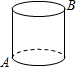 如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蚂蚁,想吃到与A点相对的上底面B处的一只已被粘住的苍蝇,这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点,则最短路程是10$\sqrt{4+{π}^{2}}$cm.(结果用根号表示)
如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蚂蚁,想吃到与A点相对的上底面B处的一只已被粘住的苍蝇,这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点,则最短路程是10$\sqrt{4+{π}^{2}}$cm.(结果用根号表示)
分析 要求需要爬行的最短路径首先要把圆柱的侧面积展开,得到一个矩形,然后利用勾股定理求两点间的线段即可.
解答  解:如图,把圆柱的侧面展开,得到如图所示的图形,
解:如图,把圆柱的侧面展开,得到如图所示的图形,
其中AC=πR=10πcm,BC=20cm,
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10$\sqrt{4+{π}^{2}}$cm.
故答案为:10$\sqrt{4+{π}^{2}}$cm.
点评 本题考查了平面展开-最短路径问题,解题的关键是理解要求需要爬行的最短路径首先要把圆柱的侧面积展开,底面周长和高以及所走的路线构成一个直角三角形,然后再求线段的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.两条平行线被第三条直线所截,则下列说法错误的是( )
| A. | 一对邻补角的平分线互相垂直 | B. | 一对同位角的平分线互相平行 | ||
| C. | 一对内错角的平分线互相平行 | D. | 一对同旁内角的平分线互相平行 |
10.已知a为任意实数,且M=2a-2,N=a2-1,则M,N的大小关系为( )
| A. | M≤N | B. | M≥N | C. | M=N | D. | 不能确定 |
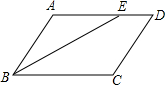 如图,?ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,?ABCD的周长20.
如图,?ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,?ABCD的周长20.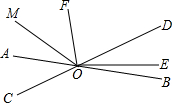 如图,直线AB,CD相交于点O,∠DOE:∠BOE=3:1,OF平分∠AOD,
如图,直线AB,CD相交于点O,∠DOE:∠BOE=3:1,OF平分∠AOD,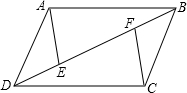 如图,已知四边形ABCD为平行四边形,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.
如图,已知四边形ABCD为平行四边形,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.