题目内容
17.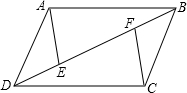 如图,已知四边形ABCD为平行四边形,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.
如图,已知四边形ABCD为平行四边形,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.(1)求证:∠DAE=∠BCF.
(2)连接AC交于BD点O,求证:AC,EF互相平分.
分析 (1)只要证明△ABE≌△CDF,即可推出∠DAE=∠BCF.
(2)只要证明四边形AECF为平行四边形即可.
解答 (1)证明:∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD,
∴∠ABD=∠CDB,
在△ABE与△CDF中
$\left\{\begin{array}{l}{AB=CD}\\{∠ABD=∠CDB}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF,
∴∠DAE=∠BCF.
(2)证明:连接AF、CE.
由(1)得,△ABE≌△CDF,
∴∠AED=∠CFB,AE=CF,
∴∠AEB=∠CFD,
∴AE∥CF,
∴四边形AECF为平行四边形,
∴AC、EF互相平分.
点评 本题考查平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7.25÷2n=22,则n的值为( )
| A. | 2 | B. | 5 | C. | 3 | D. | 4 |
2.能判断一个四边形是平行四边形的为( )
| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组对角相等 | ||
| C. | 一组对边平行,一组对角互补 | D. | 一组对边平 行,两条对角线相等 |
6.一个空间几何体的三视图,如图所示,则这个几何体的表面积为( )


| A. | $\frac{9\sqrt{3}}{4}$ | B. | 9$\sqrt{3}$ | C. | $\frac{9\sqrt{2}}{4}$ | D. | 9$\sqrt{6}$ |
19.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a6 | C. | (3m2n)2=6m4n2 | D. | a9÷a3=a3 |
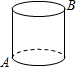 如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蚂蚁,想吃到与A点相对的上底面B处的一只已被粘住的苍蝇,这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点,则最短路程是10$\sqrt{4+{π}^{2}}$cm.(结果用根号表示)
如图所示,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蚂蚁,想吃到与A点相对的上底面B处的一只已被粘住的苍蝇,这只蚂蚁从A点出发沿着圆柱形的侧面爬到B点,则最短路程是10$\sqrt{4+{π}^{2}}$cm.(结果用根号表示)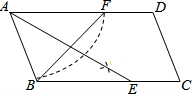 如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为8.
如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为8.