题目内容
17.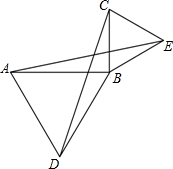 如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.
如图,已知∠ABC=90°,分别以AB和BC为边向外作等边△ABD和等边△BCE,连接AE,CD.求证:AE=CD.
分析 根据等边三角形的性质得到∠ABD=∠CBE=60°,BA=BD,BC=BE,根据角的和差得到∠CBD=∠ABE,推出△CBD≌△EBA(SAS),根据全等三角形的性质即可得到结论.
解答 证明:∵△ABD和△BCE为等边三角形,
∴∠ABD=∠CBE=60°,BA=BD,BC=BE,
∴∠ABD+∠ABC=∠CBE+∠ABC,
即∠CBD=∠ABE,
在△CBD与△EBA中,$\left\{\begin{array}{l}{BD=AB}\\{∠DBC=∠ABE}\\{BC=BE}\end{array}\right.$,
∴△CBD≌△EBA(SAS),
∴AE=CD.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
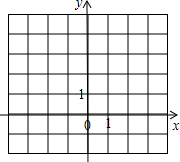 在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).
在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3). (1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.
(1)甲、乙两人用如图所示的①、②两个转盘做游戏,规则是:转动两个转盘各1次,若两个转盘停止转动后,指针所在区域的两个数字之积为奇数,则甲获胜,否则乙胜.试求出甲获胜的概率.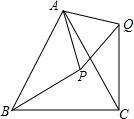 如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ. 如图,AB是⊙O的直径,D是$\widehat{BC}$的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
如图,AB是⊙O的直径,D是$\widehat{BC}$的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC并延长与DM相交于点G.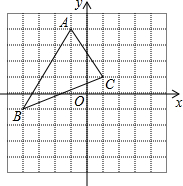 如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)
如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)